| Concept Of Trees |
The concept of a tree is probably the most important in graph theory, especially for those interested in applications of graphs.
A tree is a connected graph without any circuits. The graph in Fig 3-5 for instance, is a tree. It follows immediately from the definition that a tree has to be a simple graph, that is, having neither a self-loop nor parallel edges (because they both form circuits).
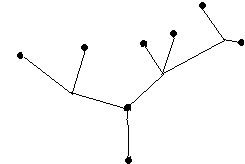Fig. 3-5. Tree
Trees appear in numerous instances. The genealogy of a family is often represented by means of a tree. A river with its tributaries and sub-tributaries can also be represented by a tree. The sorting of mail according to zip code and the sorting of punched cards are done according to a tree (called decision tree or sorting tree).
3.3.1 Some properties of Trees
There is one and only one path between every pair of vertices in a tree, T.
A tree with n vertices has n-1 edges.
Any connected graph with n vertices and n-1 edges is a tree.
A graph is a tree if and only if it is minimally connected.
Therefore a graph with n vertices is called a tree if
- G is connected and is circuit less, or
- G is connected and has n-1 edges, or
- G is circuit less and has n-1 edges, or
- There is exactly one path between every pair of vertices in G, or
- G is a minimally connected graph.
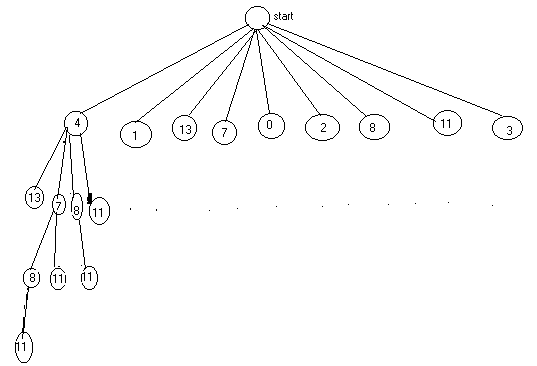Fig. 3-6 Tree of a monotonically increasing sequences in 4,1,13,7,0,2,8,11,3
3.3.2 Pendent Vertices in a Tree
It is observed that a tree shown in the Fig. 3-5 has several pendant vertices. A pendant vertex was defined as a vertex of degree one). The reason is that in a tree of n vertices we have n-1 edges, and hence 2(n-1) degrees to be divided among n vertices. Since no vertex can be of zero degree, we must have at least two vertices of degree one in a tree. This makes sense only if n ³
2.
An Application: The following problem is used in teaching computer programming. Given a sequence of integers, no two of which are the same find the largest monotonically increasing subsequence in it. Suppose that the sequence given to us is 4,1,13,7,0,2,8,11,3; it can be represented by a tree in which the vertices (except the start vertex) represent individual numbers in the sequence, and the path from the start vertex to a particular vertex v describes the monotonically increasing subsequence terminating in v.
As shown in Fig. 3-6, this sequence contains four longest monotonically increasing subsequences, that is, (4,7,8,11), (1,7,8,11), (1,2,8,11) and (0,2,8,11). Each is of length four. Computer programmers refer to such a tree used in representing data as a data tree.
3.3.3 Rooted and Binary Tree
A tree in which one vertex (called the root) is distinguished from all the others is called a rooted tree. For instance, in Fig. 3-6 vertex named start, is distinguished from the rest of the vertices. Hence vertex start can be considered the root of the tree, and so the tree is rooted. Generally, the term tree means trees without any root. However, for emphasis they are sometimes called free trees (or non rooted trees) to differentiate them from the rooted kind.
Fig. 3-6 Tree.
Binary Trees: A special class of rooted trees, called binary rooted trees, is of particular interest, since they are extensively used in the study of computer search methods, binary identification problems, and variable-length binary codes. A binary tree is defined as a tree in which there is exactly one vertex of degree two, and each of the remaining vertices of degree one or three. Since the vertex of degree two is distinct from all other vertices, this vertex serves as a root. Thus every binary tree is a rooted tree.
3.3.4 Spanning Trees
So far we have discussed the trees when it occurs as a graph by itself. Now we shall study the tree as a subgraph of another graph. A given graph has numerous subgraphs, from e edges, 2e distinct combinations are possible. Obviously, some of these subgrphs will be trees. Out of these trees we are particularly interested in certain types of trees, called spanning trees.
A tree T is said to be a spanning tree of a connected graph G if T is a subgraph of G and T contains all vertices of G. Since the vertices of G are barely hanging together in a spanning tree, it is a sort of skeleton of the original graph G. This is why a spanning tree is sometimes referred to as a skeleton or scaffolding of G. Since spanning trees are the largest trees among all trees in G, it is also quite appropriate to call a spanning tree a maximal tree subgraph or maximal tree of G.
Finding a spanning tree of a connected graph G is simple. If G has no circuit, it is its own spanning tree. If G has a circuit, delete an edge from the circuit. This will still leave the graph connected. If there are more circuits, repeat the operation till an edge from the last circuit is deleted, leaving a connected, circuit-free graph that contains all the vertices of G.
3.3.5 Hamiltonian Paths and Circuits
Hamiltonian circuit in a connected graph is defined as a closed walk that traverses every vertex of G exactly once, except of course the starting vertex, at which the walk also terminates. A circuit in a connected graph G is said to be Hamiltonian if it includes every vertex of G. Hence a Hamiltonian circuit in a graph of n vertices consists of exactly n edges.
Hamiltonian path: If we remove any one edge from a Hamiltonian circuit, we are left with a path. This path is called a Hamiltonian path. Clearly, a Hamiltonian path in a graph G traverses every vertex of G. Since a Hamiltonian path is a subgraph of a Hamiltonian circuit (which in turn is a subgraph of another graph), every graph that has a Hamiltonian circuit also has a Hamiltonian path. There are, however, many graphs with Hamiltonian paths that have no Hamiltonian circuits. The length of a Hamiltonian path in a connected graph of n vertices is n-1.
3.3.5 Traveling-Salesman Problem
A problem closely related to the question of Hamiltonian circuits is the Traveling-salesman problem, stated as follows: A salesman is required to visit a number of cities during a trip. Given the distances between the cities, in what order should he travel so as to visit every city precisely once and return home, with the minimum mileage traveled?
Representing the cities by vertices and the roads between them by edges, we get a graph. In this graph, with every edge ei there is associated a real number (the distance in miles, say), w(ei). Such a graph is called a weighted graph; w(ei) being the weight of edge ei.
In our problem, if each of the cities has a road to every other city, we have a complete weighted graph. This graph has numerous Hamiltonian circuits, and we are to pick the one that has the smallest sum of distances (or weights).
The total number of different (not edge disjoint, of course) Hamiltonian circuits in a complete graph of n vertices can be shown to be (n-1)! / 2. This follows from the fact that starting from any vertex we have n-1 edges to choose from the first vertex, n-2 from the second, n-3 from the third, and so on. These being independent, results with (n-1)! choices. This number is, however, divided by 2, because each Hamiltonian circuit has been counted twice.
Theoretically, the problem of the traveling salesman can always be solved by enumerating all (n-1)!/2 Hamiltonian circuits, calculating the distance traveled in each, and then picking the shortest one. However, for a large value of n, the labor involved is too great even for a digital computer.
The problem is to prescribe a manageable algorithm for finding the shortest route. No efficient algorithm for problems of arbitrary size has yet been found, although many attempts have been made. Since this problem has applications in operations research, some specific large-scale examples have been worked out. There are also available several heuristic methods of solution that give a route very close to the shortest one, but do not guarantee the shortest.
Exercise 3
Draw all simple graphs of one, two, three and four vertices
Name 10 situations that can be represented by means of graphs. Explain what each vertex and edge represent
Draw a connected graph that becomes disconnected when any edge is removed from it
Draw all trees of n labeled vertices for n=1,2,3,4 and 5
Sketch all binary trees with six pendent edges
Sketch all spanning trees of given graphs in this chapter
Write incidence matrix for all the graphs developed
Find the spanning trees for all the graphs developed
Draw a graph which has Hamiltonian path but does not have Hamiltonian circuit
List different paths from vertex1 to vertex n in each graph developed.
|
