| Flip Flops |
Why
Study Flip-Flops?
There are some circuits that are not quite as straight forward as the gate
circuits we have discussed in earlier lessons. However, you still
need to learn about circuits that can store and remember information.
They're the kind of circuits that are used in computers to store program
information - RAM memory.
In this lesson we'll look
at the background for those kinds of memory circuits. Our goal is
the following.

Given a flip-flop circuit,
 Determine
how the circuit will behave for a sequence of inputs.

Be able to use a flip-flop to store a single bit.
Basic
Circuit
Here's a basic circuit that involves just two NAND gates. There are
two inputs to this circuit, X and Y. Can you generate a truth table
for this circuit?
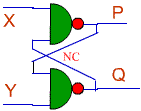
Let's
address that issue of the truth table. Here is a truth table for
you to fill in. (Print this web page if you want to work on it.)
Let's review what you know about this circuit. We can focus on what
happens when X= 0, and Y = 0, the first entry in the truth table above.
-
If X = 0, then P = 1.
We know that if either input to a NAND gate is 0, the output is 1.
-
Now. try to take advantage
of the knowledge that P = 1. If P = 1 AND Y = 0, then Q = 1.
It doesn't matter what P is, as long as Y = 0, Q will be 1.
-
That gives us the first
entry in the truth table above. Here's the truth table with what
we have figured out so far.
|
X
|
Y
|
P
|
Q
|
|
0
|
0
|
1
|
1
|
|
0
|
1
|
|
|
|
1
|
0
|
|
|
|
1
|
1
|
|
|
Now, let's address the second entry in the truth table. In that situation,
X = 0, and Y = 1.
-
If X = 0, then P = 1.
We know that if either input to a NAND gate is 0, the output is 1.
That's the same as before.
-
Now. try to take advantage
of the knowledge that P = 1. If P = 1 AND Y = 1, then Q = 0.
-
That gives us the second
entry in the truth table above. Here's the truth table with what
we have figured out so far.
|
X
|
Y
|
P
|
Q
|
|
0
|
0
|
1
|
1
|
|
0
|
1
|
1
|
0
|
|
1
|
0
|
|
|
|
1
|
1
|
|
|
Now, let's address the second entry in the truth table. In that situation,
X = 0, and Y = 1.
-
If X = 0, then P = 1.
We know that if either input to a NAND gate is 0, the output is 1.
That's the same as before.
-
Now. try to take advantage
of the knowledge that P = 1. If P = 1 AND Y = 1, then Q = 0.
-
That gives us the second
entry in the truth table above. Here's the truth table with what
we have figured out so far.
|
X
|
Y
|
P
|
Q
|
|
0
|
0
|
1
|
1
|
|
0
|
1
|
1
|
0
|
|
1
|
0
|
|
|
|
1
|
1
|
|
|
|