Introduction
- Why Do You Want to Learn This Material?
In this lesson you're going to be introduced to Digital
Logic. There are lots of reasons to learn digital logic.
Here are some of those reasons.
-
Digital logic is the foundation
for digital computers. If you want to understand the innards of computers
you need to know digital logic.
-
Digital logic has relations
to other kinds of logic including:
-
Formal logic - as taught
by many philosophy departments
-
Fuzzy logic - a tool used
to design control systems and many other systems.
-
So, in learning digital
logic you learn something that helps you elsewhere.
-
For many students, learning
digital logic is fun.
What
Are You Going to Learn?
There are at least two general areas you need to become familiar with.
-
First, there's background
you need to know - the basics of digital logic - things like zeros and
ones (0s and 1s) and how you can represent signals as sequences of zeroes
and ones. Eventually you will want to know how large arrays of zeroes
and ones can be used in computer files to store information in pictures,
documents, sounds and even movies and you'll want to learn about how information
can be transmitted, between computers and digital signal sources.
-
You will also need to
know things about digital circuits - gates, flip-flops and memory elements
and others - so that you can eventually design circuits to manipulate digital
signals.
Here is a short list of the topics you will
learn.
-
Learn what logic signals
look like
-
Model logic signals
-
Learn Boolean algebra
for logic analysis
-
Learn about gates that
process logic signals
-
Learn how to design some
smaller logic circuits
-
Learn about flip-flops
and memory elements that store logic signals
Objectives
For This Lesson
Here's what we are after in this lesson
- what you should be able to do.

Given a system that uses logic signals

Be able to specify what the output will be when the input is zero (0) and
what the output will be when the input is one (1).

Given an AND, OR, NAND or NOT gate,

Be able to determine the output of the gate given the input logic signals.

Given a system that requires gates,

Be able to wire a chip correctly, and to check that the chip is functioning
properly.
Logic
Signals
There are a number of different systems for representing binary information
in physical systems. Here are a few.
-
A voltage signal with
zero
(0) corresponding to
0 volts and
one
(1) corresponding to five
or three volts.
-
A sinusoidal signal with
zero corresponding to some frequency, and one corresponding to some other
frequency.
-
A current signal with
zero corresponding to 4 milliamps
and one corresponding to 20 milliamps.
-
And one last way is to
use switches, OPEN
for "0" and CLOSED
for "1".
-
(And there are more ways!)
Characteristics
of Logic Signals
We should note that all of these signals can and usually will change in
time, so that we really are looking at dynamic situations. However,
we will start by looking at these signals as though they were not changing
in time.
-
We will pick a voltage
signal as a working example. It can take on two values corresponding
to 0 and 1.
-
We can associate a variable
with that logic signal, and we can assign a symbol to represent that variable
- like the symbol A.
Think
Binary!
Let's examine a typical situation. You have some sort of device that
generates a logic signal.
-
It could be a telephone
that converts your voice signal into a sequence of zeros and ones.
-
It could be the thermostat
on the wall that generates a 1 when the temperature is too low, and a 0
when the temperature is above the set point temperature.
The
logic signal, A, takes on values of 0
(FALSE, OFF) or 1 (TRUE, ON).
That signal might really be a voltage, a switch closure, etc. However,
we want to think in terms of zeros and ones, not in terms of the values
of the voltage.
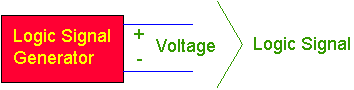
Operations
on Logic Signals
Once we have the concept of a logic signal we can talk about operations
that can be performed on logic signals. Begin by assuming we have
two logic signals, A and B.
Then assume that those two signals form an input set to some circuit that
takes two logic signals as inputs, and has an output that is also a logic
signal. That situation is represented below.

The
output, C, depends upon the inputs, A and B. There are many different
ways that C could depend upon A and B. The output, C, is a function,
- a logic function - of the inputs, A and B. IWe will examine a few
basic logic functions - AND, OR
and NOT functions and start learning the circuitry
that you use to implement those functions.
Logic
Gates
If we think of two signals, A and B, as representing a truth
value of two different propositions, then A could be either TRUE
(a logical 1) or FALSE (a logical
0).
B can take on the same values. Now consider a situation in which
the output, C, is TRUE only when both A is TRUE and B is TRUE. We
can construct a truth table for this situation.
In that truth table, we insert all of the possible combinations of inputs,
A and B, and for every combination of A and B we list the output, C.
A |
B |
C |
False |
False |
False |
False |
True |
False |
True |
False |
False |
True |
True |
True |
An AND Example
Let's imagine a physician prescribing two drugs. For some conditions
drug A is prescribed, and for other conditions
drug B is prescribed. Taken separately
each drug is safe. When used together dangerous side effects are
produced.
Let
-
A = Truth of the statement
"Drug
'A' is prescribed.".
-
B = Truth of the statement
"Drug
'B' is prescribed.".
-
C = Truth of the statement
"The
patient is in danger.".
Then, the truth table
below shows when the patient is in danger.
A |
B |
C |
False |
False |
False |
False |
True |
False |
True |
False |
False |
True |
True |
True |
Notice that C is TRUE when both A AND B are
true and only then!
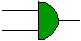
AND
GATES
An AND function can be implemented electrically using a device known as
an AND gate. You might imagine a system in which zero (0) is represented
by zero (0) volts, and one (1) is represented by three (3) volts, for example.
If we are going to use electrical devices we need some sort of symbolic
representation. There is a standard symbol for an AND gate shown
below.
Often in lab work it's helpful to use an LED to show when a signal is 0
or 1. Usually a 1
is indicated with an LED that is ON (i.e. glowing). You can use the
buttons below to check out this AND gate (Note what an AND gate symbol
looks like!) with a simulated LED. Note the following in the simulation
(and you can use this in your lab experiments).
|

