Logic
Functions
In the first lesson on digital logic we examined how you could use truth
tables and gates to produce an electrical implementation of a given truth
table. In this lesson you will examine that process more formally.
Larger logic problems require a systematic approach for solution.
Modern integrated circuit chips - for example CPU chips for personal computers
- can use millions of logic devices. The sheer magnitude of these
designs is a clear sign that a formal approach to the design is needed.
In this lesson you will learn some ways of using Boolean algebra expressions
that point directly to a particular logic circuit implementation.
We will finish the lesson by examining a way to simplify circuits so that
they use a minimum number of components and gates.
Here are your goals for this lesson - what you should be able to
do.

Given a Boolean function described by a truth table,

Be able to determine the smallest sum of products
function that has the same truth table.

Be able to determine the AND-OR-NOT
circuit that implements that smallest sum of products function.

Be able to determine the all-NAND
circuit that implements that smallest sum
of products function.
Minterm
Expansions
There are usually numerous ways any Boolean function can be expressed,
and each expression leads fairly naturally to a circuit with AND gates,
OR gates and inverters. Different ways of expressing a function can
have widely varying levels of complexity. More complex circuits will
require more gates and inverters, so it's a reasonable goal to learn how
to devise circuits that are as simple as possible.
In this section we are going to look at how you can represent circuits
differently using Boolean algebra. We'll move from that to a consideration
of how you can implement circuits based on different Boolean expressions.
Those concepts are important because any given circuit, even one as complex
as a CPU chip, will be better if you can design it to use fewer components.
That's expecially important in large circuits involving millions of transistors
or gates. Savings of a small percentage of components can translate
into thousands of transistors or gates.
An Example Function
Let's look at a simple Boolean function of three variables. We'll
describe this function with a truth table. Here's the truth table.
The input variables are X, Y and Z, and the function output is F.
|
X
|
Y
|
Z
|
F
|
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
0
|
|
0
|
1
|
0
|
1
|
|
0
|
1
|
1
|
0
|
|
1
|
0
|
0
|
0
|
|
1
|
0
|
1
|
1
|
|
1
|
1
|
0
|
0
|
|
1
|
1
|
1
|
0
|
Let's examine this function in some detail. The only non-zero entries
are at:
X = 0, Y = 1,
Z = 0
and
X = 1, Y
= 0, Z = 1
The function
is 1 for those
two input conditions and zero for all other input conditions.
Now, lets' think about how we can implement this function. Here's
a description of what we want to implement:
This word statement is very close to the function we want. We've
highlighted the important aspects of the function. Here's the function:
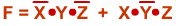
This function is read as (NOT-X AND Y AND
NOT-Z) OR (X AND NOT-Y AND Z) and when we
read NOT-X that
means we have to have X=0
to make the three terms ANDed
together work out to 1.
Now, let's look at a circuit that will implement this function. Here's
the circuit. Notice how the inputs are grouped into groups of 3,
ANDed together (after taking inverses where appropriate) and the results
ORed at the end.
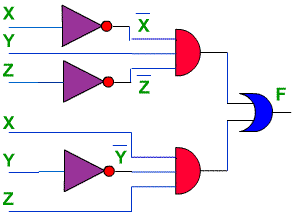
Defining
Minterms
In producing our circuit we had to use the form:
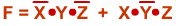
. This form is
composed of two groups of three. Each group of three is a minterm.
What the expression minterm
is intended to imply it that each of the groups of three in the expression
takes on a value of 1
only for one of the eight possible combinations of X, Y and Z and their
inverses. Important points about minterms include the following.
|

