SYSTEMS OF EQUATIONS in TWO VARIABLES
A system of equations is a collection of two or more equations with the same
set of unknowns. In solving a system of equations, we try to find values for
each of the unknowns that will satisfy every equation in the system.
The equations in the system can be linear or non-linear. This tutorial reviews
systems of linear equations.
A problem can be expressed in narrative form or the problem can be expressed in
algebraic form.
Let's start with an example stated in narrative form. We'll convert it to an
equivalent equation in algebraic form, and then we will solve it.
Example 1:
A total of $12,000 is invested in two funds paying 9% and 11% simple interest.
If the yearly interest is $1,180, how much of the $12,000 is invested at each
rate?
Before you work this problem, you must know the definition of simple interest.
Simple interest can be calculated by multiplying the amount invested at the
interest rate.
Solution:
We have two unknowns: the amount of money invested at 9% and the amount of
money invested at 11%. Our objective is to find these two numbers.
Sentence (1) ''A total of $12,000 is invested in two funds paying 9% and 11%
simple interest.'' can be restated as (The amount of money invested at 9%)
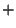 (The amount of money invested at 11%)
(The amount of money invested at 11%)
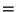 $12,000.
$12,000.
Sentence (2) ''If the yearly interest is $1,180, how much of the $12,000 is
invested at each rate?'' can be restated as (The amount of money invested at 9%)
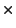 9% + (The amount of money invested at 11%
9% + (The amount of money invested at 11%
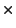 11%)
11%)
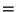 total interest of $1,180.
total interest of $1,180.
It is going to get tiresome writing the two phrases (The amount of money
invested at 9%) and (The amount of money invested at 11%) over and over again.
So let's write them in shortcut form. Call the phrase (The amount of money
invested at 9%) by the symbol
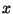 and call the phrase (The amount of money invested at 11% times 11%) by the
symbol
and call the phrase (The amount of money invested at 11% times 11%) by the
symbol
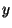 . .
Let's rewrite sentences (1) and (2) in shortcut form.
We have converted a narrative statement of the problem to an equivalent
algebraic statement of the problem. Let's solve this system of equations.
A system of linear equations can be solved four different ways:
Substitution,
Elimination,
Matrices,
Graphing.
The Method of Substitution:
The method of substitution involves five steps:
Step 1: Solve for y in equation (1).
Step 2: Substitute this value for y in equation (2). This will change equation
(2) to an equation with just one variable, x.
Step 3: Solve for x in the translated equation (2).
Step 4: Substitute this value of x in the y equation you obtained in Step 1.
Step 5: Check your answers by substituting the values of x and y in each of the
original equations. If, after the substitution, the left side of the equation
equals the right side of the equation, you know that your answers are correct.
The Method of Elimination:
The process of elimination involves five steps:
In a two-variable problem rewrite the equations so that when the equations are
added, one of the variables is eliminated, and then solve for the remaining
variable.
Step 1: Change equation (1) by multiplying equation (1) by
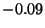 to obtain a new and equivalent equation (1).
to obtain a new and equivalent equation (1).
Step 2: Add new equation (1) to equation (2) to obtain equation (3).
Step 3: Substitute
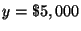 in equation (1) and solve for x.
in equation (1) and solve for x.
Step 4: Check your answers in equation (2). Does
The Method of Matrices:
This method is essentially a shortcut for the method of elimination.
Rewrite equations (1) and (2) without the variables and operators. The left
column contains the coefficients of the x's, the middle column contains the
coefficients of the y's, and the right column contains the constants.
The objective is to reorganize the original matrix into one that looks like
where a and b are the solutions to the system.
Step 1. Manipulate the matrix so that the number in cell 11 (row 1-col 1) is 1.
In this case, we don't have to do anything. The number 1 is already in the cell.
Step 2: Manipulate the matrix so that the number in cell 21 is 0. To do this we
rewrite the matrix by keeping row 1 and creating a new row 2 by adding -0.09 x
row 1 to row 2.
Step 3: Manipulate the matrix so that the cell 22 is 1. Do this by multiplying
row 2 by 50.
Step 4: Manipulate the matrix so that cell 12 is 0. Do this by adding
You can read the answers off the matrix as x = $7,000 and y = $5,000.
|

