Systems of Linear Equations: Gaussian Elimination
It is quite hard to solve non-linear systems of equations, while linear
systems are quite easy to study. There are numerical techniques which help to
approximate nonlinear systems with linear ones in the hope that the solutions of
the linear systems are close enough to the solutions of the nonlinear systems.
We will not discuss this here. Instead, we will focus our attention on linear
systems.
For the sake of simplicity, we will restrict ourselves to three, at most
four, unknowns. The reader interested in the case of more unknowns may easily
extend the following ideas.
Definition. The equation
a x + b y + c z + d w = h
where a, b, c, d, and h are known numbers,
while x, y, z, and w are unknown numbers, is called
a linear equation. If h =0, the linear equation is said to be
homogeneous. A linear system is a set of linear equations and a
homogeneous linear system is a set of homogeneous linear equations.
For example,
and
are linear systems, while
is a nonlinear system (because of y2). The system
is an homogeneous linear system.
Matrix Representation of a Linear System
Matrices are helpful in rewriting a linear system in a very simple form. The
algebraic properties of matrices may then be used to solve systems. First,
consider the linear system
Set the matrices
Using matrix multiplications, we can rewrite the linear system above as the
matrix equation
As you can see this is far nicer than the equations. But sometimes it is worth
to solve the system directly without going through the matrix form. The matrix
A is called the matrix coefficient of the linear system. The matrix C
is called the nonhomogeneous term. When
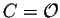 ,
the linear system is homogeneous. The matrix X is the unknown matrix. Its
entries are the unknowns of the linear system. The augmented matrix
associated with the system is the matrix [A|C], where ,
the linear system is homogeneous. The matrix X is the unknown matrix. Its
entries are the unknowns of the linear system. The augmented matrix
associated with the system is the matrix [A|C], where
In general if the linear system has n equations with m unknowns, then the
matrix coefficient will be a nxm matrix and the augmented matrix an nx(m+1)
matrix. Now we turn our attention to the solutions of a system.
Definition. Two linear systems with n unknowns are said to be
equivalent if and only if they have the same set of solutions.
This definition is important since the idea behind solving a system is to
find an equivalent system which is easy to solve. You may wonder how we will
come up with such system? Easy, we do that through elementary operations.
Indeed, it is clear that if we interchange two equations, the new system is
still equivalent to the old one. If we multiply an equation with a nonzero
number, we obtain a new system still equivalent to old one. And finally
replacing one equation with the sum of two equations, we again obtain an
equivalent system. These operations are called elementary operations on
systems. Let us see how it works in a particular case.
Example. Consider the linear system
The idea is to keep the first equation and work on the last two. In doing
that, we will try to kill one of the unknowns and solve for the other two. For
example, if we keep the first and second equation, and subtract the first one
from the last one, we get the equivalent system
Next we keep the first and the last equation, and we subtract the first from the
second. We get the equivalent system
Now we focus on the second and the third equation. We repeat the same procedure.
Try to kill one of the two unknowns (y or z). Indeed, we keep the
first and second equation, and we add the second to the third after multiplying
it by 3. We get
This obviously implies z = -2. From the second equation, we get y
= -2, and finally from the first equation we get x = 4. Therefore the
linear system has one solution
Going from the last equation to the first while solving for the unknowns is
called backsolving.
Keep in mind that linear systems for which the matrix coefficient is
upper-triangular are easy to solve. This is particularly true, if the matrix is
in echelon form. So the trick is to perform elementary operations to transform
the initial linear system into another one for which the coefficient matrix is
in echelon form.
Using our knowledge about matrices, is there anyway we can rewrite what we did
above in matrix form which will make our notation (or representation) easier?
Indeed, consider the augmented matrix
Let us perform some elementary row operations on this matrix. Indeed, if we keep
the first and second row, and subtract the first one from the last one we get
Next we keep the first and the last rows, and we subtract the first from the
second. We get
Then we keep the first and second row, and we add the second to the third after
multiplying it by 3 to get
This is a triangular matrix which is not in echelon form. The linear system for
which this matrix is an augmented one is
As you can see we obtained the same system as before. In fact, we followed the
same elementary operations performed above. In every step the new matrix was
exactly the augmented matrix associated to the new system. This shows that
instead of writing the systems over and over again, it is easy to play around
with the elementary row operations and once we obtain a triangular matrix, write
the associated linear system and then solve it. This is known as Gaussian
Elimination. Let us summarize the procedure:
Gaussian Elimination. Consider a linear system.
- 1.
- Construct the augmented matrix for the system;
- 2.
- Use elementary row operations to transform the augmented matrix into a
triangular one;
- 3.
- Write down the new linear system for which the triangular matrix is the
associated augmented matrix;
- 4.
- Solve the new system. You may need to assign some parametric values to
some unknowns, and then apply the method of back substitution to solve the
new system.
Example. Solve the following system via Gaussian elimination
The augmented matrix is
We use elementary row operations to transform this matrix into a triangular one.
We keep the first row and use it to produce all zeros elsewhere in the first
column. We have
Next we keep the first and second row and try to have zeros in the second
column. We get
Next we keep the first three rows. We add the last one to the third to get
This is a triangular matrix. Its associated system is
Clearly we have v = 1. Set z=s and w=t, then
we have
The first equation implies
Using algebraic manipulations, we get
x = -
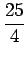
-
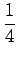 s s
- t.
Putting all the stuff together, we have
Example. Use Gaussian elimination to solve the linear system
The associated augmented matrix is
We keep the first row and subtract the first row multiplied by 2 from the second
row. We get
This is a triangular matrix. The associated system is
Clearly the second equation implies that this system has no solution. Therefore
this linear system has no solution.
Definition. A linear system is called inconsistent or
overdetermined if it does not have a solution. In other words, the set of
solutions is empty. Otherwise the linear system is called consistent.
Following the example above, we see that if we perform elementary row
operations on the augmented matrix of the system and get a matrix with one of
its rows equal to
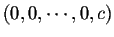 ,
where ,
where
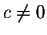 ,
then the system is inconsistent. ,
then the system is inconsistent.
|

