Fluid Mechanics

Introduction

A fluid is a substance that deforms continuously when subjected to a tangential or shear stress, however small the shear stress may be. Such a continuous deformation under the stress constitutes a flow. Fluid mechanics is therefore the study of mechanics of such matter. As such, this pertains mostly to the study of liquids and gases, however the general theories may be applied to the study of amorphous solids, colloidal suspensions and gelatinous materials.

Fluid mechanics is a subdivision of continuum mechanics. Consequentially, fluids are considered continuous media for analysis, and their discrete nature is of no consequence for most applications. This assumption is valid mostly on length scales much larger than intramolecular distances. The departure from continuum is characterised by a dimensionless parameter, the Knudsen Number, defined by K_n = λ / L, where L is a characteristic length scale of the flow. The continuum hypothesis holds good if Kn < 0.01. However, recent applications in nanotechnology and biotechnology are demonstrating that the governing equations are still relevant on smaller scales, specifically when they are modified to include the effects of electrostatic, magnetic, colloidal and surface-tension driven forces.

Some fluid mechanics problems can be solved by applying conservation laws (mass, momentum, energy) of mechanics to a finite control volume. However, in general, it is necessary to apply those laws to an infintesimal control volume, then use the resulting differential equations. Additionally, boundary values, initial conditions and thermodynamic state equations are generally necessary to obtain numeric or analytic solutions.

Fluid Properties

In addition to the properties like mass, velocity, and pressure usually considered in physical problems, the following are the basic properties of a fluid:

Density

The density of a fluid is defined as the mass per unit volume of the fluid over an infinitesimal volume.

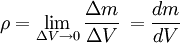
Viscosity

Viscosity (represented by μ) is a material property, unique to fluids, that measures the fluid's resistance to flow. Though this is a property of the fluid, its effect is understood only when the fluid is in motion. When different elements move with different velocities, then the each element tries to drag its neighbouring elements along with it. Thus shear stress can be identified between fluid elements of different velocities.

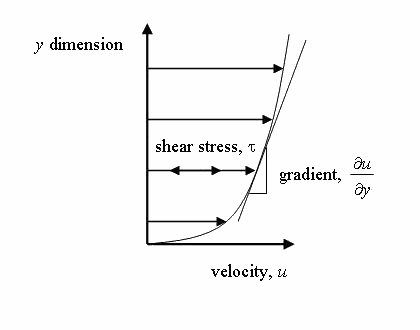
Velocity gradient in laminar shear flow

The relationship between the shear stress and the velocity field was studied by Isaac Newton and he proposed that the shear stresses are directly proportional to the velocity gradient.

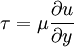
The constant of proportionality is called the coefficient of dynamic viscosity.

Another coefficient, known as the kinematic viscosity is defined as the ratio of dynamic viscosity and density. ν = μ / ρ

Reynolds Number

There are several dimensionless parameters that are important in fluid dynamics. Reynolds number (after Osborne Reynolds, 1842-1912) is an important parameter in the study of fluid flows. Physically it is the ratio between inertial and viscous forces. The value of Reynolds number determines the kind of flow of the fluid.

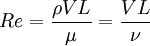
where ρ(rho) is the density, μ(mu) is the viscosity, V is the velocity of the flow, and L is the dimension representing length for the flow. Additionally, we define a parameter ν(nu) as the kinematic viscosity.

Low Re indicates creeping flow, medium Re is laminar flow, and high Re indicates turbulent flow.

Reynolds number can also be transformed to take account of different flow conditions. For example the reynolds number for flow within a pipe is expressed as

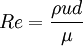
where u is the average fluid velocity within the pipe and d is the inside diameter of the pipe.

Application of dynamic forces (and the Reynolds number) to the real world: sky-diving, where friction forces equal the falling body's weight. (jjam)

Pathlines and Streamlines

The path which a fluid element traces out in space is called a pathline. For steady non fluctuating flows where a pathline is followed continuously by a number of fluid elements , the pathline is called streamline. A streamline is the imaginary line whose tangent gives the velocity of flow at all times if the flow is steady, however in an unsteady flow, the streamline is constantly changing and thus the tangent gives the velocity of an element at an instant of time. A common practice in analysis is taking some of the walls of a control volume to be along streamlines. Since there is no flow perpendicular to streamlines, only the flow across the other boundaries need be considered.

Hydrostatics

The pressure distribution in a fluid under gravity is given by the relation dp/dz = −ρg where dz is the change in the direction of the gravitational field (usually in the vertical direction). Note that it is quite straightforward to get the relations for arbitrary fields too, for instance, the pseudo field due to rotation.

The pressure in a fluid acts equally in all directions. When it comes in contact with a surface, the force due to pressure acts normal to the surface. The force on a small area dA is given by p dA where the force is in the direction normal to dA. The total force on the area A is given by the vector sum of all these infinitesimal forces.

Control Volume Analysis

A fluid dynamic system can be analysed using a control volume, which is an imaginary surface enclosing a volume of interest. The control volume can be fixed or moving, and it can be rigid or deformable. Thus, we will have to write the most general case of the laws of mechanics to deal with control volumes.

The first equation we can write is the conservation of mass over time. Consider a system where mass flow is given by dm/dt, where m is the mass of the system. We have,

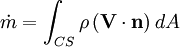
For steady flow, we have

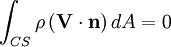
And for incompressible flow, we have

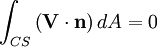
If we consider flow through a tube, we have, for steady flow,

ρ₁A₁V₁ = ρ₂A₂V₂

and for incompressible steady flow, A₁V₁ = A₂V₂.

Law of conservation of momentum as applied to a control volume states that

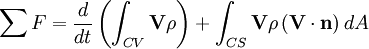
where V is the velocity vector and n is the unit vector normal to the control surface at that point.

Law of Conservation of Energy (First Law of Thermodynamics)

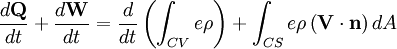
where e is the energy per unit mass.

Bernoulli's Equation

Bernoulli's equation considers frictionless flow along a streamline.

For steady, incompressible flow along a streamline, we have

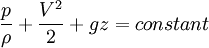
We see that Bernoulli's equation is just the law of conservation of energy without the heat transfer and work.

It may seem that Bernoulli's equation can only be applied in a very limited set of situations, as it requires ideal conditions. However, since the equation applies to streamlines, we can consider a streamline near the area of interest where it is satisfied, and it might still give good results, i.e., you don't need a control volume for the actual analysis (although one is used in the derivation of the equation).

Energy in terms of Head

Bernoulli's equation can be recast as

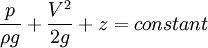
This constant can be called head of the water, and is a representation of the amount of work that can be extracted from it. For example, for water in a dam, at the inlet of the penstock, the pressure is high, but the velocity is low, while at the outlet, the pressure is low (atmospheric) while the velocity is high. The value of head calculated above remains constant (ignoring frictional losses).