Historical approaches
Until the rise of space travel in the twentieth century, there was little distinction between orbital and
celestial mechanics. The fundamental techniques, such as those used to solve the
Keplerian problem, are therefore the same in both fields. Furthermore, the
history of the fields is almost entirely shared.
Kepler's equation
Kepler was the first to successfully
model planetary orbits to a high degree of accuracy.
Derivation
To compute the position of a satellite at a given time (the Keplerian
problem) is a difficult problem. The opposite problem�to compute the
time-of-flight given the starting and ending positions�is simpler. We present a
derivation for the time-of-flight equation here.
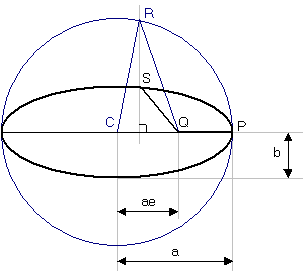
Kepler's construction for deriving the time-of-flight equation. The
bold ellipse is the satellite's orbit, with the star or planet at
one focus Q. The goal is to compute the time required for a
satellite to travel from
periapsis P to a given point S. Kepler
circumscribed the blue auxiliary circle around the ellipse,
and used it to derive his time-of-flight equation in terms of
eccentric anomaly.
The problem is to find the time t at
which the satellite reaches point S, given
that it is at
periapsis P at time
t = 0. We are given that the
semimajor axis of the orbit is a, and
the
semiminor axis is b; the
eccentricity is e, and the planet is at
Q, at a distance of
ae from the center C of the
ellipse.
The key construction that will allow us to analyse this situation is the
auxiliary circle (shown in blue) circumscribed on the orbital ellipse. This
circle is taller than the ellipse by a factor of a
/ b in the direction of the minor axis, so all area measures on
the circle are magnified by a factor of a / b
with respect to the analogous area measures on the ellipse.
Any given point on the ellipse can be mapped to the corresponding point on
the circle that is a / b further from
the ellipse's major axis. If we do this mapping for the position
S of the satellite at time
t, we arrive at a point
R on the circumscribed circle. Kepler
defines the angle PCR to be the
eccentric anomaly angle E. (Kepler's
terminology often refers to angles as "anomalies".) This definition makes the
time-of-flight equation easier to derive than it would be using the
true
anomaly angle PQS.
To compute the time-of-flight from this construction, we note that
Kepler's second law allows us to compute time-of-flight from the area swept
out by the satellite, and so we will set about computing the area
PQS swept out by the satellite.
First, the area PQR is a magnified
version of the area PQS:
-
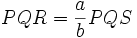
Furthermore, area PQS is the area swept
out by the satellite in time t. We know
that, in one orbital period T, the satellite
sweeps out the whole area πab of the orbital
ellipse. PQS is the
t / T fraction of this area, and substituting, we arrive at
this expression for PQR:
-
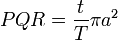
Second, the area PQR is also formed by
removing area QCR from
PCR:
-
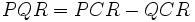
Area PCR is a fraction of the
circumscribed circle, whose total area is πa2.
The fraction is E / 2π, thus:
-
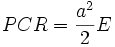
Meanwhile, area QCR is a triangle whose
base is the
line
segment QC of length
ae, and whose height is
asinE:
-
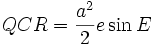
Combining all of the above:
-
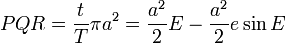
Dividing through by a2 / 2:
-
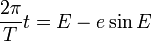
To understand the significance of this formula, consider an analogous formula
giving an angle M during circular motion
with constant angular velocity n:
-
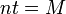
Setting n = 2π / T and
M = E − esinE gives us
Kepler's equation. Kepler referred to n as
the mean motion, and E − esinE
as the mean anomaly. The term "mean" in this case refers to the fact that
we have "averaged" the satellite's non-constant angular velocity over an entire
period to make the satellite's motion amenable to analysis. All satellites
traverse an angle of 2π per orbital period
T, so the mean angular velocity is always
2π / T.
Substituting n into the formula we
derived above gives this:
-
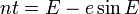
This formula is commonly referred to as Kepler's equation.
Application
With Kepler's formula, finding the time-of-flight to reach an angle (true
anomaly) of θ from periapsis is broken into two
steps:
- Compute the eccentric anomaly E from
true anomaly θ
- Compute the time-of-flight t from
the eccentric anomaly E
Finding the angle at a given time is harder. Kepler's equation is
transcendental in E, meaning it cannot
be solved for E analytically, and so
numerical approaches must be used. In effect, one must guess a value of
E and solve for time-of-flight; then adjust
E as necessary to bring the computed
time-of-flight closer to the desired value until the required precision is
achieved. Usually,
Newton's method is used to achieve relatively fast convergence.
The main difficulty with this approach is that it can take prohibitively long
to converge for the extreme elliptical orbits. For near-parabolic orbits,
eccentricity e is nearly 1, and plugging
e = 1 into the formula for mean anomaly,
E − sinE, we find ourselves
subtracting two nearly-equal values, and so accuracy suffers. For near-circular
orbits, it is hard to find the periapsis in the first place (and truly circular
orbits have no periapsis at all). Furthermore, the equation was derived on the
assumption of an elliptical orbit, and so it does not hold for parabolic or
hyperbolic orbits at all. These difficulties are what led to the development of
the universal variable formulation, described below.
Perturbation theory One can deal with perturbations just by summing the forces and integrating,
but that is not always best. Historically, variation of parameters has
been used which is easier to mathematically apply with when perturbations are
small.
|

