Laws of astrodynamics
The fundamental laws of astrodynamics are
Newton's law of universal gravitation and
Newton's laws of motion, while the fundamental mathematical tool is his
differential
calculus.
Standard assumptions in astrodynamics include non-interference from outside
bodies, negligible mass for one of the bodies, and negligible other forces (such
as from the solar wind, atmospheric drag, etc.). More accurate calculations can
be made without these simplifying assumptions, but they are more complicated.
The increased accuracy often does not make enough of a difference in the
calculation to be worthwhile.
Kepler's laws of planetary motion may be derived from Newton's laws, when it
is assumed that the orbiting body is subject only to the gravitational force of
the central attractor. When an engine thrust or propulsive force is present,
Newton's laws still apply, but Kepler's laws are invalidated. When the thrust
stops, the resulting orbit will be different but will once again be described by
Kepler's laws.
Escape velocity
The formula for
escape velocity is easily derived as follows. The
specific energy (energy per unit
mass) of any space
vehicle is composed of two components, the specific
potential energy and the specific
kinetic energy. The specific potential energy associated with a planet of
mass M is
given by
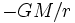
while the
specific kinetic energy of an object is given by
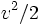
Since
energy is conserved, the total
specific orbital energy
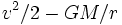
does not depend on the distance, r, from
the center of the central body to the space vehicle in question. Therefore, the
object can reach infinite r only if this
quantity is nonnegative, which implies
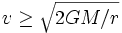
The escape velocity from the Earth's surface is about 11 km/s, but that is
insufficient to send the body an infinite distance because of the gravitational
pull of the Sun. To escape the solar system from the vicinity of the Earth
requires around 42 km/s velocity, but there will be "part credit" for the
Earth's orbital velocity for spacecraft launched from Earth, if their further
acceleration (due to the propulsion system) carries them in the same direction
as Earth travels in its orbit.
Formulae for free orbits
Orbits are
conic
sections, so, naturally, the formula for the distance of a body for a given
angle corresponds to the formula for that curve in
polar coordinates, which is:
-
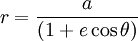 . .
The parameters are given by the
orbital elements.
Circular orbits
Although most orbits are elliptical in nature, a special case is the circular
orbit, which is an ellipse of zero eccentricity. The formula for the velocity of
a body in a circular orbit at distance r from the center of gravity of
mass M is
-
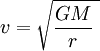
where G is the
gravitational constant, equal to
- 6.672 598 � 10−11 m3/(kg�s2)
To properly use this formula, the units must be consistent; for example, M
must be in kilograms, and r must be in meters. The answer will be in
meters per second.
The quantity GM is often termed the
standard gravitational parameter, which has a different value for every
planet or moon in the
solar system.
Once the circular orbital velocity is known, the
escape velocity is easily found by multiplying by the square root of 2:
-
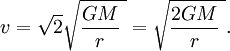
|