Fluid mechanics
Fluid mechanics is the study of how
fluids move and
the forces on
them. (Fluids include
liquids and
gases.) Fluid
mechanics can be divided into
fluid
statics, the study of fluids at rest, and
fluid dynamics, the study of fluids in motion. It is a branch of
continuum mechanics, a subject which models matter without using the
information that it is made out of atoms. The study of fluid mechanics goes back
at least to the days of ancient Greece, when
Archimedes
made a beginning on fluid statics. However, fluid mechanics, especially fluid
dynamics, is an active field of research with many unsolved or partly solved
problems. Fluid mechanics can be mathematically complex. Sometimes it can best
be solved by
numerical methods, typically using computers. A modern discipline, called
Computational Fluid Dynamics (CFD), is devoted to this approach to
solving fluid mechanics problems. Also taking advantage of the highly visual
nature of fluid flow is
Particle Image Velocimetry, an experimental method for visualizing and
analyzing fluid flow.
Relationship to continuum mechanics
Fluid mechanics is a subdiscipline of
continuum mechanics, as illustrated in the following table.
|
Continuum mechanics the study of the physics of continuous materials |
Solid mechanics: the study of the physics of continuous materials
with a defined rest shape. |
Elasticity: which describes materials that return to their rest
shape after an applied
stress. |
|
Plasticity: which describes materials that permanently deform after
a large enough applied stress. |
Rheology: the study of materials with both solid and fluid
characteristics |
| Fluid mechanics: the study of the
physics of continuous materials which take the shape of their container. |
Non-Newtonian fluids |
|
Newtonian fluids |
In a mechanical view, a fluid is a substance that does not support
tangential stress; that is why a fluid at rest has the shape of its
containing vessel. A fluid at rest has no shear stress.
Assumptions
Like any mathematical model of the real world, fluid mechanics makes some
basic assumptions about the materials being studied. These assumptions are
turned into equations that must be satisfied if the assumptions are to hold
true. For example, consider an incompressible fluid in three dimensions. The
assumption that mass is conserved means that for any fixed closed surface (such
as a sphere) the rate of mass passing from outside to inside the
surface must be the same as rate of mass passing the other way. (Alternatively,
the mass inside remains constant, as does the mass outside). This
can be turned into an
integral equation over the surface.
Fluid mechanics assumes that every fluid obeys the following:
-
Conservation of mass
-
Conservation of momentum
- The continuum hypothesis, detailed below.
Further, it is often useful (and realistic) to assume a fluid is
incompressible - that is, the density of the fluid does not change. Liquids
can often be modelled as incompressible fluids, whereas gases cannot.
Similarly, it can sometimes be assumed that the
viscosity
of the fluid is zero (the fluid is inviscid). Gases can often be assumed
to be inviscid. If a fluid is viscous, and its flow contained in some way (e.g.
in a pipe), then
the flow at the boundary must have zero velocity. For a viscous fluid, if the
boundary is not porous, the shear forces between the fluid and the boundary
results also in a zero velocity for the fluid at the boundary. This is called
the
no-slip condition. For a porous media otherwise, in the frontier of the
containing vessel, the slip condition is not zero velocity, and the fluid has a
discontinuous velocity field between the free fluid and the fluid in the porous
media (this is related to the
Beavers and Joseph condition).
The continuum hypothesis
Fluids are composed of
molecules that collide with one another and solid objects. The continuum
assumption, however, considers fluids to be
continuous. That is, properties such as density, pressure, temperature, and
velocity are taken to be well-defined at "infinitely" small points, defining a
REV (Reference Element of Volume), at the geometric order of the distance
between two adjacent molecules of fluid. Properties are assumed to vary
continuously from one point to another, and are averaged values in the REV. The
fact that the fluid is made up of discrete molecules is ignored.
The continuum hypothesis is basically an approximation, in the same way
planets are approximated by point particles when dealing with celestial
mechanics, and therefore results in approximate solutions. Consequently,
assumption of the continuum hypothesis can lead to results which are not of
desired accuracy. That said, under the right circumstances, the continuum
hypothesis produces extremely accurate results.
Those problems for which the continuum hypothesis does not allow solutions of
desired accuracy are solved using
statistical mechanics. To determine whether or not to use conventional fluid
dynamics or statistical mechanics, the
Knudsen number is evaluated for the problem. The Knudsen number is defined
as the ratio of the molecular
mean free path length to a certain representative physical length
scale. This length scale could be, for example, the radius of a body in a
fluid. (More simply, the Knudsen number is how many times its own diameter a
particle will travel on average before hitting another particle). Problems with
Knudsen numbers at or above
unity
are best evaluated using statistical mechanics for reliable solutions.
Navier-Stokes equations
The Navier-Stokes equations (named after
Claude-Louis Navier and
George Gabriel Stokes) are the set of equations that describe the motion of
fluid substances
such as liquids and gases. These equations state that changes in
momentum (acceleration)
of fluid particles depend only on the external
pressure
and internal viscous forces (similar to
friction)
acting on the fluid. Thus, the Navier-Stokes equations describe the balance of
forces acting at any given region of the fluid.
The Navier-Stokes equations are
differential equations which describe the motion of a fluid. Such equations
establish relations among the rates of change the variables of interest. For
example, the Navier-Stokes equations for an ideal fluid with zero viscosity
states that acceleration (the rate of change of velocity) is proportional to the
derivative of internal pressure.
This means that solutions of the Navier-Stokes equations for a given physical
problem must be sought with the help of
calculus.
In practical terms only the simplest cases can be solved exactly in this way.
These cases generally involve non-turbulent, steady flow (flow does not change
with time) in which the
Reynolds number is small.
For more complex situations, such as global weather systems like El Niņo or
lift in a wing, solutions of the Navier-Stokes equations can currently only be
found with the help of computers. This is a field of sciences by its own called
computational fluid dynamics.
General form of the equation
The general form of the Navier-Stokes equations for the conservation of
momentum is:
-
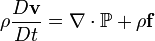
where
-
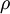is the fluid density,
-
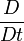is the
substantive derivative (also called the material derivative),
-
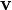is the velocity vector,
-
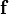is the body force vector, and
-
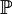is a tensor
that represents the surface forces applied on a fluid particle (the
comoving
stress tensor).
Unless the fluid is made up of spinning degrees of freedom like vortices,
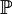is a symmetric tensor. In general, (in three dimensions)
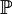has the form:
-
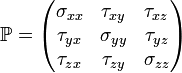
where
-
are normal stresses, and
-
are tangential stresses (shear stresses).
The above is actually a set of three equations, one per dimension. By
themselves, these aren't sufficient to produce a solution. However, adding
conservation of mass and appropriate boundary conditions to the system of
equations produces a solvable set of equations.
Newtonian vs. non-Newtonian fluids
A Newtonian fluid (named after
Isaac
Newton) is defined to be a
fluid whose
shear
stress is linearly proportional to the
velocity
gradient in
the direction
perpendicular to the plane of shear. This definition means regardless of the
forces acting on a fluid, it continues to flow. For example, water is a
Newtonian fluid, because it continues to display fluid properties no matter how
much it is stirred or mixed. A slightly less rigorous definition is that the
drag of a small object being moved through the fluid is proportional to the
force applied to the object. (Compare
friction).
By contrast, stirring a
non-Newtonian fluid can leave a "hole" behind. This will gradually fill up
over time - this behaviour is seen in materials such as pudding,
oobleck, or
sand (although sand
isn't strictly a fluid). Alternatively, stirring a non-Newtonian fluid can cause
the viscosity to decrease, so the fluid appears "thinner" (this is seen in
non-drip paints).
There are many types of non-Newtonian fluids, as they are defined to be
something that fails to obey a particular property.
Equations for a Newtonian fluid
The constant of proportionality between the shear stress and the velocity
gradient is known as the
viscosity.
A simple equation to describe Newtonian fluid behaviour is
-
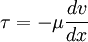
where
- τ is the shear stress exerted by the fluid
("drag")
- μ is the fluid viscosity - a constant of
proportionality
-
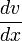is the velocity gradient perpendicular to the direction of shear
For a Newtonian fluid, the viscosity, by definition, depends only on
temperature and
pressure,
not on the forces acting upon it. If the fluid is
incompressible and viscosity is constant across the fluid, the equation
governing the shear stress (in
Cartesian coordinates) is
-
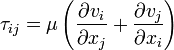
where
- τij is the shear stress
on the ith face of a
fluid element in the jth
direction
- vi is the velocity
in the ith direction
- xj is the
jth direction
coordinate
If a fluid does not obey this relation, it is termed a
non-Newtonian fluid, of which there are several types.
|
Print
