Notation, language, and rigor
Most of the mathematical notation in use today was not invented until the
16th
century.
Before that, mathematics was written out in words, a painstaking process that
limited mathematical discovery. In the
18th
century,
Euler was responsible for many of the notations in use today. Modern
notation makes mathematics much easier for the professional, but beginners often
find it daunting. It is extremely compressed: a few symbols contain a great deal
of information. Like musical notation, modern mathematical notation has a strict
syntax and encodes information that would be difficult to write in any other
way.
Mathematical
language also is hard for beginners. Words such as or and only
have more precise meanings than in everyday speech. Also confusing to beginners,
words such as
open
and
field have been given specialized mathematical meanings.
Mathematical jargon includes technical terms such as
homeomorphism and
integrable. But there is a reason for special notation and technical
jargon: mathematics requires more precision than everyday speech. Mathematicians
refer to this precision of language and logic as "rigor".
Rigor is fundamentally a matter of
mathematical proof. Mathematicians want their theorems to follow from axioms
by means of systematic reasoning. This is to avoid mistaken "theorems",
based on fallible intuitions, of which many instances have occurred in the
history of the subject.
The level of rigor expected in mathematics has varied over time: the Greeks
expected detailed arguments, but at the time of
Isaac
Newton the methods employed were less rigorous. Problems inherent in the
definitions used by Newton would lead to a resurgence of careful analysis and
formal proof in the 19th century. Today, mathematicians continue to argue among
themselves about
computer-assisted proofs. Since large computations are hard to verify, such
proofs may not be sufficiently rigorous.
Axioms in
traditional thought were "self-evident truths", but that conception is
problematic. At a formal level, an axiom is just a string of
symbols, which has an intrinsic meaning only in the context of all derivable
formulas of an
axiomatic system. It was the goal of
Hilbert's program to put all of mathematics on a firm axiomatic basis, but
according to
G�del's incompleteness theorem every (sufficiently powerful) axiomatic
system has
undecidable formulas; and so a final
axiomatization of mathematics is impossible. Nonetheless mathematics is
often imagined to be (as far as its formal content) nothing but
set theory
in some axiomatization, in the sense that every mathematical statement or proof
could be cast into formulas within set theory.
Mathematics as science
Carl Friedrich Gauss referred to mathematics as "the Queen of the Sciences".
In the original Latin Regina Scientiarum, as well as in
German K�nigin der Wissenschaften, the word corresponding to
science means (field of) knowledge. Indeed, this is also the original
meaning in English, and there is no doubt that mathematics is in this sense a
science. The specialization restricting the meaning to natural science is
of later date. If one considers
science to be
strictly about the physical world, then mathematics, or at least
pure mathematics, is not a science.
Albert Einstein has stated that "as far as the laws of mathematics refer
to reality, they are not certain; and as far as they are certain, they do not
refer to reality."
Many philosophers believe that mathematics is not experimentally
falsifiable,[citation
needed] and thus not a science according to the definition
of Karl
Popper. However, in the 1930s important work in mathematical logic showed
that mathematics cannot be reduced to logic, and Karl Popper concluded that
"most mathematical theories are, like those of physics and biology,
hypothetico-deductive: pure mathematics therefore turns out to be much closer to
the natural sciences whose hypotheses are conjectures, than it seemed even
recently."
Other thinkers, notably
Imre
Lakatos, have applied a version of falsificationism to mathematics itself.
An alternative view is that certain scientific fields (such as
theoretical physics) are mathematics with axioms that are intended to
correspond to reality. In fact, the theoretical physicist,
J. M. Ziman, proposed that science is public knowledge and thus
includes mathematics.
In any case, mathematics shares much in common with many fields in the physical
sciences, notably the exploration of the logical consequences of assumptions.
Intuition and
experimentation also play a role in the formulation of
conjectures
in both mathematics and the (other) sciences.
Experimental mathematics continues to grow in importance within mathematics,
and computation and simulation are playing an increasing role in both the
sciences and mathematics, weakening the objection that mathematics does not use
the
scientific method. In his 2002 book
A New Kind of Science,
Stephen Wolfram argues that computational mathematics deserves to be
explored empirically as a scientific field in its own right.
The opinions of mathematicians on this matter are varied. Many mathematicians
feel that to call their area a science is to downplay the importance of its
aesthetic side, and its history in the traditional seven
liberal
arts; others feel that to ignore its connection to the sciences is to turn a
blind eye to the fact that the interface between mathematics and its
applications in science and
engineering has driven much development in mathematics. One way this
difference of viewpoint plays out is in the philosophical debate as to whether
mathematics is created (as in art) or discovered (as in science).
It is common to see
universities divided into sections that include a division of Science and
Mathematics, indicating that the fields are seen as being allied but that
they do not coincide. In practice, mathematicians are typically grouped with
scientists at the gross level but separated at finer levels. This is one of many
issues considered in the
philosophy of mathematics.
Mathematical awards are generally kept separate from their equivalents in
science. The most prestigious award in mathematics is the
Fields Medal,
established in 1936 and now awarded every 4 years. It is often considered,
misleadingly, the equivalent of science's
Nobel
Prizes. The
Wolf Prize in Mathematics, instituted in 1979, recognizes lifetime
achievement, and another major international award, the
Abel Prize,
was introduced in 2003. These are awarded for a particular body of work, which
may be innovation, or resolution of an outstanding problem in an established
field. A famous list of 23 such open problems, called "Hilbert's
problems", was compiled in 1900 by German mathematician
David
Hilbert. This list achieved great celebrity among mathematicians, and at
least nine of the problems have now been solved. A new list of seven important
problems, titled the "Millennium
Prize Problems", was published in 2000. Solution of each of these problems
carries a $1 million reward, and only one (the
Riemann hypothesis) is duplicated in Hilbert's problems.
Fields of mathematics
As noted above, the major disciplines within mathematics first arose out of
the need to do calculations in commerce, to understand the relationships between
numbers, to measure land, and to predict
astronomical
events. These four needs can be roughly related to the broad subdivision of
mathematics into the study of quantity, structure, space, and change (i.e.,
arithmetic,
algebra,
geometry,
and
analysis). In addition to these main concerns, there are also subdivisions
dedicated to exploring links from the heart of mathematics to other fields: to
logic, to
set theory
(foundations),
to the empirical mathematics of the various sciences (applied
mathematics), and more recently to the rigorous study of
uncertainty.
Quantity
The study of quantity starts with
numbers, first
the familiar
natural numbers and
integers
("whole numbers") and arithmetical operations on them, which are characterized
in
arithmetic. The deeper properties of integers are studied in
number theory, whence such popular results as
Fermat's last theorem. Number theory also holds two widely-considered
unsolved problems: the
twin prime conjecture and
Goldbach's conjecture.
As the number system is further developed, the integers are recognized as a
subset of the
rational numbers ("fractions").
These, in turn, are contained within the
real
numbers, which are used to represent continuous quantities. Real numbers are
generalized to
complex numbers. These are the first steps of a hierarchy of numbers that
goes on to include
quarternions and
octonions.
Consideration of the natural numbers also leads to the
transfinite numbers, which formalize the concept of counting to infinity.
Another area of study is size, which leads to the
cardinal numbers and then to another conception of infinity: the
aleph
numbers, which allow meaningful comparison of the size of infinitely large
sets.

Natural numbers |
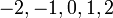
Integers |
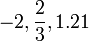
Rational numbers
|
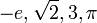
Real numbers |
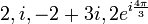
Complex numbers |
|

