Physics
Operation
In all rockets, the exhaust is formed from
propellants
carried within the rocket prior to use.
Rocket thrust is due to the rocket engine, which propels the rocket forwards by
exhausting the propellant rearwards at extreme high speed.
In a closed chamber, the pressures are equal in each direction and no
acceleration occurs. If an opening is provided at the bottom of the chamber then
the pressure is no longer acting on that side. The remaining pressures give a
resultant thrust on the side opposite the opening; as well as permitting exhaust
to escape. Using a nozzle increases the forces further, in fact multiplies the
thrust as a function of the area ratio of the nozzle, since the pressures also
act on the nozzle. As a side effect the pressures act on the exhaust in the
opposite direction and accelerate this to very high speeds (in accordance with
Newton's Third Law).
If propellant gas is continuously added to the chamber then this
disequilibrium of pressures can be maintained for as long as propellant remains.
It turns out (from
conservation of momentum) that the speed of the exhaust of a rocket
determines how much momentum increase is created for a given amount of
propellant, and this is termed a rocket's
specific impulse.
As the remaining propellant decreases, the vehicle's becomes lighter and
acceleration tends to increase until eventually it runs out of propellant, and
this means that much of the speed change occurs towards the end of the burn when
the vehicle is much lighter.
Forces on a rocket in flight
The general study of the forces on a rocket or other spacecraft is called
astrodynamics.
Flying rockets are primarily affected by the following:
- Thrust
from the engine(s)
-
Gravity from
celestial bodies
-
Drag if moving in the atmosphere
-
Lift; usually relatively small effect except for
rocket-powered aircraft
In addition, the
inertia/centrifugal pseudo-force can be significant due to the path of the
rocket around the center of a celestial body; when high enough speeds in the
right direction and altitude are achieved a stable
orbit or
escape velocity is obtained.
During a rocket launch, there is a point of maximum aerodynamic drag called
Max Q. This
determines the minimum aerodynamic strength of the vehicle.
These forces, with a stabilizing tail present will, unless deliberate control
efforts are made, to naturally cause the vehicle to follow a trajectory termed a
gravity
turn, and this trajectory is often used at least during the initial part of
a
launch. This means that the vehicle can maintain low or even zero
angle of attack. This minimizes transverse
stress on the launch vehicle; allowing for a weaker, and thus lighter,
launch vehicle.
Net thrust
The thrust of a rocket is often deliberately varied over a flight, to provide
a way to control the airspeed of the vehicle so as to minimize aerodynamic
losses but also so as to limit
g-forces
that would otherwise occur during the flight as the propellant mass decreases,
which could damage the vehicle, crew or payload.
Below is an approximate equation for calculating the gross thrust of a
rocket:
-
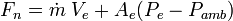
where:
-
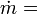 propellant
flow (kg/s or lb/s) propellant
flow (kg/s or lb/s)
-
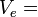 jet
velocity at nozzle exit plane (m/s or s) jet
velocity at nozzle exit plane (m/s or s)
-
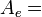 flow
area at nozzle exit plane (m2 or ft2) flow
area at nozzle exit plane (m2 or ft2)
-
 static
pressure at nozzle exit plane (Pa or lb/ft2) static
pressure at nozzle exit plane (Pa or lb/ft2)
-
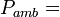 ambient
(or atmospheric) pressure (Pa or lb/ft2) ambient
(or atmospheric) pressure (Pa or lb/ft2)
Since, unlike a jet engine, a conventional rocket motor lacks an air intake,
there is no 'ram drag' to deduct from the gross thrust. Consequently the net
thrust of a rocket motor is equal to the gross thrust.
The
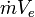 term represents the momentum thrust, which remains constant at a given throttle
setting, whereas the
term represents the momentum thrust, which remains constant at a given throttle
setting, whereas the
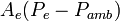 term represents the pressure thrust term. At full throttle, the net thrust of a
rocket motor improves slightly with increasing altitude, because the reducing
atmospheric pressure increases the pressure thrust term.
term represents the pressure thrust term. At full throttle, the net thrust of a
rocket motor improves slightly with increasing altitude, because the reducing
atmospheric pressure increases the pressure thrust term.
Specific impulse
As can be seen from the thrust equation the effective speed of the exhaust,
Ve, has a large impact on the amount of thrust produced from a particular
quantity of fuel burnt per second. The thrust-seconds (impulse)
per unit of propellant is called
Specific Impulse (Isp) or effective exhaust velocity and this is one of the
most important figures that describes a rocket's performance.
Vacuum Isp
Due to the specific impulse varying with pressure, a quantity that is easy to
compare and calculate with is useful. Because rockets
choke
at the throat, and because the supersonic exhaust prevents external pressure
influences travelling upstream, it turns out that the pressure at the exit is
ideally exactly proportional to the propellant flow
 ,
provided the mixture ratios and combustion efficiencies are maintained. It is
thus quite usual to rearrange the above equation slightly: ,
provided the mixture ratios and combustion efficiencies are maintained. It is
thus quite usual to rearrange the above equation slightly:
-
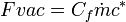
and so define the vacuum Isp to be:
- Vevac = Cfc
*
Where:
-
 the speed of sound constant at the throat
the speed of sound constant at the throat
-
 the thrust coefficient constant of the nozzle (typically between 0.8 and
1.9)
the thrust coefficient constant of the nozzle (typically between 0.8 and
1.9)
And hence:
-

Delta-v (rocket equation)
The delta-v
capacity of a rocket is the theoretical total change in velocity that a rocket
can achieve without any external interference (without air drag or gravity or
other forces).
The delta-v that a rocket vehicle can provide can be calculated from the
Tsiolkovsky rocket equation:
-
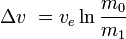
where:
- m0 is the initial total
mass, including propellant, in kg (or lb)
- m1 is the final total
mass in kg (or lb)
- ve is the
effective exhaust velocity in m/s or (ft/s) or
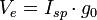
-
 is the delta-v in m/s (or ft/s)
is the delta-v in m/s (or ft/s)
Delta-v can also be calculated for a particular manoeuvre; for example the
delta-v to launch from the surface of the Earth to
Low earth orbit is about 9.7 km/s, which leaves the vehicle with a sideways
speed of about 7.8 km/s at an altitude of around 200 km. In this manoeuvre about
1.9 km/s is lost in air drag, gravity drag and gaining altitude.
Mass ratios
Mass ratio is the ratio between the initial fuelled mass and the mass after
the 'burn'.
Everything else being equal, a high mass ratio is desirable for good
performance, since it indicates that the rocket is lightweight and hence
performs better, for essentially the same reasons that low weight is desirable
in sports cars.
Rockets as a group have the highest
thrust-to-weight ratio of any type of engine; and this helps vehicles
achieve high
mass ratios,
which improves the performance of flights. The higher this ratio, the less
engine mass is needed to be carried and permits the carrying of even more
propellant, this enormously improves performance.
Achievable mass ratios are highly dependent on many factors such as
propellant type, the design of engine the vehicle uses, structural safety
margins and construction techniques.
| Vehicle |
Takeoff Mass |
Final Mass |
Mass ratio |
Mass fraction |
|
Ariane 5 (vehicle + payload) |
746,000 kg |
2,700 kg + 16,000 kg |
39.9 |
0.975 |
|
Titan 23G first stage |
258,000 lb (117,020 kg) |
10,500 lb (4,760 kg) |
24.6 |
0.959 |
|
Saturn V |
3,038,500 kg |
13,300 kg + 118,000 kg |
23.1 |
0.957 |
|
Space Shuttle (vehicle + payload) |
2,040,000 kg |
104,000 kg + 28,800 kg |
15.4 |
0.935 |
|
Saturn 1B (stage only) |
448,648 kg |
41,594 kg |
10.7 |
0.907 |
|
V2 |
12.8 ton (13000 kg) |
|
3.85 |
0.74 |
|
X-15 |
34,000 lb (15,420 kg) |
14,600 lb (6,620 kg) |
2.3 |
0.57 |
|
Concorde |
400,000 lb |
|
2 |
0.5 |
| 747 |
800,000 lb |
|
2 |
0.5 |
Staging
Often, the required velocity (delta-v) for a mission is unattainable by any
single rocket because the
propellant,
tankage, structure,
guidance, valves and engines and so on, take a particular minimum percentage
of take-off mass.
The mass ratios that can be achieved with a single set of fixed rocket
engines and tankage varies depends on acceleration required, construction
materials, tank layout, engine type and propellants used, but for example the
first stage of the Saturn V, carrying the weight of the upper stages, was able
to achieve a mass ratio of about 10.
This problem is frequently solved by
staging � the rocket sheds excess weight (usually empty tankage and
associated engines) during launch to reduce its weight and effectively increase
its mass
ratio. Staging is either serial where the rockets light after the
previous stage has fallen away, or parallel, where rockets are burning
together and then detach when they burn out.
Typically, the acceleration of a rocket increases with time (if the thrust
stays the same) as the weight of the rocket decreases as propellant is burned.
Discontinuities in acceleration will occur when stages burn out, often starting
at a lower acceleration with each new stage firing.
Energy efficiency
Rocket launch vehicles take-off with a great deal of flames, noise and drama,
and it might seem obvious that they are grievously inefficient. However while
they are far from perfect, their energy efficiency is not as bad as might be
supposed.
The energy density of rocket propellant is around 1/3 that of conventional
hydrocarbon fuels; the bulk of the mass is in the form of (often relatively
inexpensive) oxidiser. Nevertheless, at take-off the rocket has a great deal of
energy in the form of fuel and oxidiser stored within the vehicle, and it is of
course desirable that as much of the energy stored in the propellant ends up as
kinetic or
potential energy of the body of the rocket as possible.
Energy from the fuel is lost in air drag and
gravity
drag and is used to gain altitude. However, much of the lost energy ends up
in the exhaust.
100% efficiency within the engine (ηc)
would mean that all of the heat energy of the combustion products is converted
into kinetic energy of the jet.
This is not possible, but the
high expansion ratio nozzles that can be used with rockets come surprisingly
close: when the nozzle expands the gas, the gas is cooled and accelerated, and
an energy efficiency of up to 70% can be achieved. Most of the rest is heat
energy in the exhaust that is not recovered.
This compares very well with other engine designs. The high efficiency is
a consequence of the fact that rocket combustion can be performed at very high
temperatures and the gas is finally released at much lower temperatures, and so
giving good
Carnot efficiency.
However, engine efficiency is not the whole story. In common with many
jet-based
engines, but particularly in rockets due to their high and typically fixed
exhaust speeds, rocket vehicles are extremely inefficient at low speeds
irrespective of the engine efficiency. The problem is that at low speeds, the
exhaust carries away a huge amount of
kinetic energy rearward. This phenomenon is termed
propulsive efficiency (ηp).
However, as speeds rise, the resultant exhaust speed goes down, and the
overall vehicle energetic efficiency rises, reaching a peak of around 100% of
the engine efficiency when the vehicle is travelling exactly at the same speed
that the exhaust is emitted. In this case the exhaust would ideally stop dead in
space behind the moving vehicle, taking away zero energy, and from conservation
of energy, all the energy would end up in the vehicle. The efficiency then drops
off again at even higher speeds as the exhaust ends up travelling forwards
behind the vehicle.
From these principles it can be shown that the propulsive efficiency
ηp for a rocket moving at speed
u with an exhaust velocity
c is:
-

And the overall energy efficiency η is:
- η = ηpηc
Since the energy ultimately comes from fuel, these joint considerations mean
that rockets are mainly useful when a very high speed is required, such as
ICBMs or
orbital launch, and they are rarely if ever used for general aviation. For
example, from the equation, with an ηc
of 0.7, a rocket flying at Mach 0.85 (which most aircraft cruise at) with an
exhaust velocity of Mach 10, would have a predicted overall energy efficiency of
5.9%, whereas a conventional, modern, air breathing jet engine achieves closer
to 30% or more efficiency. Thus a rocket would need about 5x more energy; and
allowing for the ~3x lower specific energy of rocket propellant than
conventional air fuel, roughly 15x more mass of propellant would need to be
carried for the same journey.
Thus jet engines which have a better match between speed and jet exhaust
speed such as
turbofans (in spite of their worse ηc)
dominate for subsonic and supersonic atmospheric use while rockets work best at
hypersonic speeds. On the other hand rockets do also see many short-range
relatively low speed military applications where their low-speed
inefficiency is outweighed by their extremely high thrust and hence high
accelerations.
Safety, reliability and accidents
Rockets are not inherently highly dangerous. In military usage quite adequate
reliability is obtained.
Because of the enormous chemical energy in all useful
rocket propellants (greater energy per weight than explosives, but lower
than gasoline),
accidents can and have happened. The number of people injured or killed is
usually small because of the great care typically taken, but this record is not
perfect.
|

