The Kinetic Theory
This brief summary is abridged from a more detailed
discussion to be found in Quinn's "Temperature"About
the same time that thermodynamics was evolving,
James Clerk Maxwell (1831-1879) and
Ludwig Boltzmann
(1844-1906) developed a theory describing the way molecules moved -
molecular dynamics. The molecules that make up a perfect gas move about,
colliding with each other like billiard balls and bouncing off the surface
of the container holding the gas. The energy associated with motion is
called Kinetic Energy and this kinetic approach to the behavior of ideal
gases led to an interpretation of the concept of temperature on a
microscopic scale.
The amount of kinetic energy each molecule has is a function of its
velocity; for the large number of molecules in a gas (even at low pressure),
there should be a range of velocities at any instant of time. The magnitude
of the velocities of the various particles should vary greatly - no two
particles should be expected to have the exact same velocity. Some may be
moving very fast; others, quite slowly. Maxwell found that he could
represent the distribution of velocities statistically by a function known
as the Maxwellian
distribution. The collisions of the molecules with their container gives
rise to the pressure of the gas. By considering the average force exerted by
the molecular collisions on the wall, Boltzmann was able to show that the
average kinetic energy of the molecules was directly comparable to the
measured pressure, and the greater the average kinetic energy, the greater
the pressure. From Boyles' Law, we know that the pressure is directly
proportional to the temperature, therefore, it was shown that the kinetic
energy of the molecules related directly to the temperature of the gas. A
simple relation holds for this:
average kinetic energy of molecules=3kT/2,
where k is the
Boltzmann constant. Temperature is a measure of the energy of thermal
motion and, at a temperature of zero, the energy reaches a minimum (quantum
mechanically, the zero-point motion remains at 0 K).
In July, 1995, physicists in Boulder, Colo.achieved a temperature far
lower than has ever been produced before and created an entirely new state
of matter predicted decades ago by
Albert Einstein and
Satyendra Nath Bose. The
press release describes
the nature of this experiment and a full description of this phenomenon is
described by the
University of
Colorado's BEC Homepage.
Dealing with a system which contained huge numbers of molecules requires
a statistical approach to the problem. About 1902,
J. W. Gibbs (1839-1903)
introduced statistical mechanics with which he demonstrated how
average values of the properties of a system could be predicted from an
analysis of the most probable values of these properties found from a large
number of identical systems (called an ensemble). Again, in the statistical
mechanical interpretation of thermodynamics, the key parameter is identified
with a temperature which can be directly linked to the thermodynamic
temperature, with the temperature of Maxwell's distribution, and with the
perfect gas law.
Temperature becomes a quantity definable either in terms of macroscopic
thermodynamic quantities such as heat and work, or, with equal validity
and identical results, in terms of a quantity which characterized the
energy distribution among the particles in a system. (Quinn,
"Temperature")
With this understanding of the concept of temperature, it is possible to
explain how heat (thermal energy) flows from one body to another. Thermal
energy is carried by the molecules in the form of their motions and some of
it, through molecular collisions, is transferred to molecules of a second
object when put in contact with it. This mechanism for transferring thermal
energy by contact is called conduction.
A second mechanism of heat transport is illustrated by a pot of water set
to boil on a stove - hotter water closest to the flame will rise to mix with
cooler water near the top of the pot. Convection involves the bodily
movement of the more energetic molecules in a liquid or gas.
The third way that heat energy can be transferred from one body to
another is by radiation; this is the way that the sun warms the earth. The
radiation flows from the sun to the earth, where some of it is absorbed,
heating the surface.
A major dilemma in physics since the time of Newton was how to explain
the nature of this radiation.
Thermal Radiation
The nature of radiation has puzzled scientists for centuries.
Maxwell proposed that this form of energy travels as a vibratory electric
and magnetic disturbance through space in a direction perpendicular to those
disturbances.
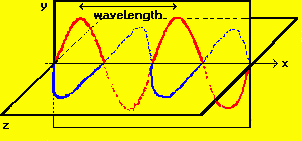
In the diagram, the electric (red) and magnetic (blue)
oscillations are orthogonal to each other - the electric lying in the xy
plane; the magnetic, in the xz plane. The wave is traveling in the x
direction. An electromagnetic wave can be defined in terms of the frequency
of its oscillation, designated by the Greek letter nu (v). The wave
moves in a straight line with with a constant speed (designated as c if it
is moving through a vacuum); the distance between successive 'peaks' of the
wave is the wavelength,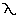 ,of the
wave and is equal to its speed divided by its frequency. ,of the
wave and is equal to its speed divided by its frequency.
The electromagnetic spectrum covers an enormous range in
wavelengths, from very short waves to very long ones.
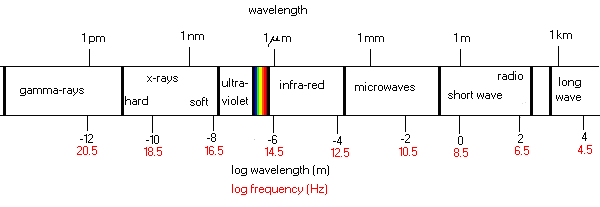
The only region of the electromagnetic spectrum to which our
eye is sensitive is the "visible" range identified in the diagram by the
rainbow colors.
The sun is not the only object that provides radiant energy;
any object whose temperature is greater than 0 K will emit some radiant
energy. The challenge to scientists was to show how this radiant energy is
related to the temperature of the object.
If an object is placed in a container whose walls are at a
uniform temperature, we expect the object to come into thermal equilibrium
with the walls of the enclosure and the object should emit radiant energy
just like the walls of the container. Such an object absorbs and radiates
the same amount of energy. Now a blackened surface absorbs all radiation
incident upon it and it must radiate in the same manner if it is in thermal
equilibrium. Equilibrium thermal radiation is therefore called black body
radiation.
The first relation between temperature and radiant energy
was deduced by J. Stefan in 1884 and theoretically explained by Boltzmann
about the same time. It states:

where the total energy is per unit area per second emitted
by the back body, T is its absolute (thermodynamic) temperature and
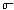 is the Stefan-Boltzmann
constant. is the Stefan-Boltzmann
constant.
The great question at the turn of the century was to explain
the way this total radiant energy emitted by a black body was spread out
into the various frequencies or wavelengths of the radiation. Maxwell's
"classical" theory of electromagnetic oscillators failed to explain the
observed brightness distribution. It was left to
Max Planck to solve the
dilemma by showing that the energy of the oscillators must be quantized,
i.e. the energies can not take any value but must change in steps, the size
of each step, or quantum, is proportional to the frequency of the oscillator
and equal to hv, where h is the Planck constant. With this
assumption, Planck derived the brightness distribution of a black body and
showed that it is defined by its temperature. Once the temperature of a
black body is specified, the Planck law can be used to calculate the
intensity of the light emitted by the body as a function of wavelength.
Conversely, if the brightness distribution of a radiating body is measured,
then, by fitting a Planck
curve to it, its temperature can be determined.
The curves illustrated below show that the hotter the body is, the
brighter it is at shorter wavelengths. The surface temperature of the sun is
6000 K, and its Planck curve peaks in the visible wavelength range. For
bodies cooler than the sun, the peak of the Planck curve shifts to longer
wavelengths, until a temperature is reached such that very little radiant
energy is emitted in the visible range.
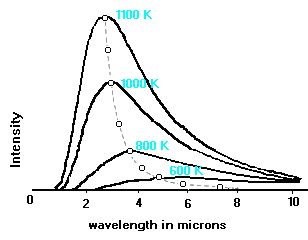 This figure
(adapted from Adkins' "Thermal Physics") shows several Planck curves for
black bodies. The Intensity is in units of energy per unit area per unit
solid angle per unit time per unit wavelength interval. The broken line
illustrates the variation with wavelength and temperature of the peaks of
the curves. This figure
(adapted from Adkins' "Thermal Physics") shows several Planck curves for
black bodies. The Intensity is in units of energy per unit area per unit
solid angle per unit time per unit wavelength interval. The broken line
illustrates the variation with wavelength and temperature of the peaks of
the curves.This is a graphical representation of Wien's law, which
states:
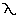 (max) ~ 0.29/T, (max) ~ 0.29/T,
where 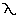 (max) is the
wavelength of maximum brightness in cm and T is the absolute temperature of
the black body. (max) is the
wavelength of maximum brightness in cm and T is the absolute temperature of
the black body.
The human body has a temperature of about 310 K and radiates primarily in
the far infrared. If a photograph of a human is taken with a camera
sensitive to this wavelength region, we get a
"thermal" picture. This
picture is courtesy of the Infrared
Processing and Analysis Center, Jet Propulsion Laboratory, NASA.
A page developed by
|

