Chemical reactions
In most cases of interest in chemical thermodynamics there are internal
degrees of freedom and processes, such as
chemical reactions and
phase transitions, which always create
entropy
unless they are at equilibrium, or are maintained at a "running equilibrium"
through "quasi-static" changes by being coupled to constraining devices, such as
pistons or
electrodes,
to deliver and receive external work. Even for homogeneous "bulk" materials, the
free energy functions depend on the
composition, as do all the
extensive
thermodynamic potentials, including the internal energy. If the quantities
{ Ni }, the number of
chemical species, are omitted from the formulae, it is impossible to
describe compositional changes.
Gibbs function
For a "bulk" (unstructured) system they are the last remaining extensive
variables. For an unstructured, homogeneous "bulk" system, there are still
various extensive compositional variables { Ni }
that G depends on, which specify the composition, the amounts of each
chemical
substance, expressed as the numbers of molecules present or (dividing by
Avogadro's number), the numbers of
moles
-
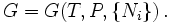
For the case where only PV work is possible
-

in which μi is the
chemical potential for the i-th
component in the system
-
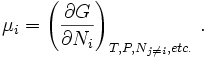
The expression for dG is especially useful at constant T and
P, conditions which are easy to achieve experimentally and which
approximates the condition in
living creatures
-

Chemical affinity
-
Main article:
Chemical affinity
While this formulation is mathematically defensible, it is not particularly
transparent since one does not simply add or remove molecules from a system.
There is always a process involved in changing the composition; e.g., a
chemical reaction (or many), or movement of molecules from one phase (liquid) to
another (gas or solid). We should find a notation which does not seem to imply
that the amounts of the components ( Ni } can be
changed independently. All real processes obey
conservation of mass, and in addition, conservation of the numbers of
atoms of each kind.
Whatever molecules are transferred to or from should be considered part of the
"system".
Consequently we introduce an explicit variable to represent the degree of
advancement of a process, a progress
variable ξ
for the
extent of reaction (Prigogine & Defay, p. 18; Prigogine, pp. 4-7;
Guggenheim, p. 37.62), and to the use of the
partial derivative ∂G/∂ξ (in place of the widely used "ΔG",
since the quantity at issue is not a finite change). The result is an
understandable
expression for the dependence of dG on
chemical reactions (or other processes). If there is just one reaction
-
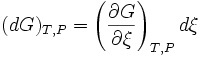
If we introduce the
stoichiometric coefficient for the i-th component in the reaction
-
-

which tells how many molecules of i are produced or consumed, we
obtain an algebraic expression for the partial derivative
-
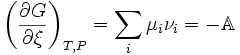
where, (De Donder; Progoine & Defay, p. 69; Guggenheim, pp. 37,240), we
introduce a concise and historical name for this quantity, the "affinity",
symbolized by A, as introduced by
Th�ophile de Donder in 1923. The minus sign comes from the fact the affinity
was defined to represent the rule that spontaneous changes will ensue only when
the change in the Gibbs free energy of the process is negative, meaning that the
chemical species have a positive affinity for each other. The differential for
G takes on a simple form which displays its dependence on compositional
change
-

If there are a number of chemical reactions going on simultaneously, as is
usually the case
-
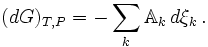
a set of reaction coordinates { ξj }, avoiding the notion
that the amounts of the components ( Ni } can be
changed independently. The expressions above are equal to zero at
thermodynamic equilibrium, while in the general case for real systems, they
are negative, due to the fact that all chemical reactions proceeding at a finite
rate produce entropy. This can be made even more explicit by introducing the
reaction rates dξj/dt. For each and every
physically independent process
(Prigogine & Defay, p. 38; Prigogine, p. 24)
-
-
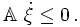
This is a remarkable result since the chemical potentials are intensive
system variables, depending only on the local molecular milieu. They cannot
"know" whether the temperature and pressure (or any other system variables) are
going to be held constant over time. It is a purely local criterion and must
hold regardless of any such constraints. Of course, it could have been obtained
by taking partial derivatives of any of the other fundamental state functions,
but nonetheless is a general criterion for (−T times) the entropy
production from that spontaneous process; or at least any part of it that is not
captured as external work. (See Constraints below.)
We now relax the requirement of a homogeneous �bulk� system by letting the
chemical potentials and the affinity apply to any locality in which a
chemical reaction (or any other process) is occurring. By accounting for the
entropy production due to irreversible processes, the inequality for dG
is now replace by an equality
-

Any decrease in the
Gibbs function of a system is the upper limit for any
isothermal,
isobaric work that can be captured in the
surroundings, or it may simply be
dissipated, appearing as T times a corresponding increase in the
entropy of the system and/or its surrounding. Or it may go partly toward doing
external work and partly toward creating entropy. The important point is that
the
extent of reaction for a chemical reaction may be coupled to the
displacement of some external mechanical or electrical quantity in such a way
that one can advance only if the other one also does. The coupling may
occasionally be rigid, but it is often flexible and variable.
Solutions
In solution
chemistry
and
biochemistry, the
Gibbs free energy decrease (∂G/∂ξ, in molar units, denoted
cryptically by ΔG) is commonly used as a surrogate for (−T times)
the entropy produced by spontaneous
chemical reactions in situations where there is no work being done; or at
least no "useful" work; i.e., other than perhaps some � PdV. The
assertion that all spontaneous reactions have a negative ΔG is merely a
restatement of the
fundamental thermodynamic relation, giving it the
physical dimensions of energy and somewhat obscuring its significance in
terms of entropy. When there is no useful work being done, it would be less
misleading to use the
Legendre transforms of the entropy appropriate for constant T, or for
constant T and P, the Massieu functions −F/T and −G/T
respectively.
|

