Balanced Realizations and model Reduction

Kalman�s canonical decomposition provides the basic theory and computational algorithm to remove unnecessary states from a realization, while preserving the input-output map. Its reliance on the controllability and observability matrices makes the approach somewhat susceptible problems, as these matrices are often poorly conditioned. A more serious drawback, however, is that reduction is based on structural properties of the system (linear independence) but without explicitly considering the quantitative aspects of the problem . in practical applications, especially when numerical commutations are involved, one is rarely faced with perfectly dependent or perfectly orthogonal vectors. Moreover, a commonly encountered problem is that of a model reduction where mides that have independent but small contributions should be eliminated. With such an objective in mind, the previous algorithm is inadequate. While the SVD of the controllability matrix can give an indication on the mides that are weekly controllable, these modes

Cannot be immediately eliminated. The reason is that they may be strongly observable and, hence, have non- negligible contribution to the system response.

In order to deal with model reduction problems, we need a quantitative approach that correctly accounts for the strength of the contribution of each mode to the system response. We discussed one such method in the first chapter via partial fraction expansions. Several several general methods for model reduction have appeared in the literature. Here we present one based on Gramians and Balanced realizations that has some interesting theoretical interpretations.

Before we with begin , let us take a look at the interpretation of the Gramians in terms of system properties. We start with the conceptually easier case of the observability Gramian where we formulate the following question; Suppose that the linear system starts at t=0 with initial condition Xo. Which states contribute more (or less) to the output energy in the interval(0,00)?

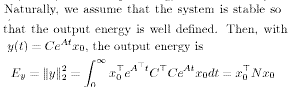
Where N is the infinite interval [0,oo] observability Gramian. Bring in the (notice that N is symmetric, implying

Consider for a moment the (similarity) state transformation X= Utx. Then in the transformed coordinates the contribution of the states to the output energy is ordered from the lowest. Furthermore if the last n � p singular values in S less that , terms of operators between vector spaces, all that we have done is to map the unit ball in the domain to a set (ellipsoid) in the co-domain. Obviously, any states associated with domain directions that map to a small semi-axis in the co-domain can be ignored without introducing a significant error.

The dual interpretation of the controllability Gramian is a little more involved. A �natural� question to ask would be much a unit-energy input contributes to the final state. For reasons that become apparent subsequently, it is convenient to consider inputs in (-oo,0) and the final state as x(0). In contrast to the observability case, the problem here is that our to be constrained on the orthogonal complement of the null space of the null space of our operator. Equivalently, we may ask the question �what is the minimum energy input that is required to produce a unit-norm final state?� in our operator framework, we look for an ellipsoid in the domain that maps to the unit ball in the co-domain. Its interpretation is naturally the opposite from the previous case. Any co-domain directions that correspond to large semi-axis of the domain ellipsoid signify weekly controllable states; these can be ignored without introducing large errors. Thus the problem at hand is to find the minimum norm input such that

Now, as in the observability case, large singular values of M correspond to small singular values of M-1 meaning directions in the state space where unit-energy inputs have effects. Consequently, through an SVD of M , we can rank the transformed states according to the energy they receive from the input.

The last step to take is to account for cases where weekly controllable modes are strongly observable and vice-versa. This would correspond to a combination of the previous two steps: the map from past inputs {- oo,0 ] to states x(0) and the map from states x(0) to future outputs [0,oo]. The composite map from the past inputs to future outputs is referred to as the system�s Hankel operator and is an alternative way to characterize the system. What is interesting here is that we can rank the states in terms of their association with the energy transfer from past inputs to future outputs. The following theorem is important:

4.6 .1 Theorem: For a stable minimal system [A,B,C,D] there exists a similarity transformation T such that in the transformed coordinates the controllability and observability Grammians are equal and diagonal. such a realization is referred to as Balanced Realization.