Robust Model Predictive Control

Robust Model Predictive Control

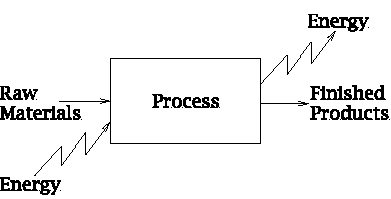
operating principles

Basic operating principles
� Operating the processing units sefly.
� Enhance the spectpled production rates.
� Enhance the product quality speciflcation.

Automatic control � Decreases process variability.
� Increases production of on-spec products.
� Decreases operator intervition.

Responsibility of the Control system � Measure the process output variables.
� Estimate the variables that are not measurable on-line.
� Decide on the corrective actions necessary
1. maintain the process at the current operating condition.
2. to hange the process from the current operating condition to onther.
� Efficiently implement the corrective actions on the process.

Overview of model predictive Control(MPC)

� Motivation for robust MPC
� Robust MPC
1. Benefits
2. cost

Model predlctlve control

1. Regulator
Find the quickest route to reach the set polnt the optimal operating condition.

2.Target calculation
Is the set point reavhable for the given constraints?
If no, what are the bessst feasible steady-state values?

3. Estimator
Outputs that are not measurable.
Unmodeled disturbances.

� A single process modle is used to forecast the process behavior.
� The optimal input trajectory minimizes the difference between the forecasted and desired process behavior.
� Able to handle physical constraints explicitly,
� There were 2233 industry applications of MPC in 1996.
� MPC is superior to traditional PID controllers because

1. able to control both measurable unmeasurable outputs.
2. able to control multivariable systems more efficiently.
3. able to handle constraints.

� The regulator, the estimator and the target calculation are all dependent on the process modle (A,B,C,),
� The controller performancae is dependent on the accuracy of the process modle.
� Plant modle mismatch may cause

1. sub-optimal controller performance.
2. closed-loop instability,
� The MPC algorithm modle:

Motivation for Rpbust MPC
� Modle uncertainty can cause closed �loop instability.
� Modle uncertainty can be caused by:
1. Unmodeled disturbances.
2. Model identification errors.

� Robust MPC explicitly accounts for model uncertainty in the controller design procedure.
� Model 1 used all data points.
� Model 2 used every other data point.

The number of branches is
� Each branch has a cost, which is the sum of deviations of the forecasted behavior from the desired behavior,
� Optimal input trajectory minimizes the deviations
For the branch with the �worst� or biggest cost.
Controller is robustly stabilizing and guarantees state convergence to the origin for all (A,B) E if there exist K
and F such that

Advantages and Disadvantages
Features Present
1. Model uncertainty is explicitly accounted for.
2. Existence of robustly stabilizing k and F guarantees state convergence to the for all

Features Missing
1.k and F do not guarantee state convergence to non-zero set points.
2.Assume the state is measurable.

Proposed Solutions
1. Use ARMAX (Auto Regressive Moving Average Exogenous Input) polytopic model uncertainty description.
2. Add integrator ARMAX model with integrator
Advantages and Disadvantages
Features present
1.Controller achieves non-zero set point tracking
2. State is measurable.

Features Missing
1. Uses input/output process models, which are less descriptive than the state-space models.
2. Controller exhibltswind-up in the presence of constraint saturation.
Proposed solutions
1. Feedback and target calculation
2. State estimation

Feedback
� If measurements are not equal the model predictions then model predictions need to be updated.
� Given measurement at time
� State measurement at time
� Update the state predictions with the disturbance models.
� Process model with disturbance modeling

Regulator with non-zero set point
� The tree trajectory models time-varying model uncertainty.
� The target calculation needs to performed at every node in the tree trajectory.
� The controllerstability id dependent on both the process dynamics and the target calculation.

Summary Designed a robust MPC control theory that
1. explicitly accounts for model uncertainty.
2. uses many models to forecast process behavior.
3. able to handle constraints without wind-up in the presence of constraint saturation.
4. achieves offset free non-zero set point tracking control.
5.is computationally intensive but manageable for small processes.