In a real suspension the particle positions are not fixed, so that the
particles are able to change their relative positions. This renders the
calculation of the settling velocities difficult, because we must know the
particle distribution to determine the average particle velocity
 ,
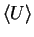which is defined by
 |
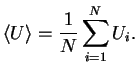(1.32) |
For monodisperse suspensions the particle distribution is not known a priori. We
must distinguish between two cases
- 1.
- The particles are so small that the continuum hypothesis is only
partially fulfilled. Then the particles show an erratic random motion, the
so called Brownian motion.
- 2.
- The particles are large enough so that the Brownian motion is neglegible.
The so called P�clet number
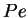provides an estimate whether the Brownian motion of particles may be neglected.
The P�clet number compares the ratio of heat advection to heat conduction and is
defined by
 |
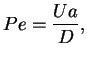(1.33) |
where
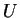is a typical velocity of the particle,
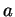its radius and
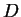is the thermal diffusion coefficient. For
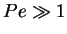the advective motion of the particle dominates and the Brownian motion can be
neglected, whereas for
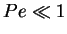the Brownian motion is dominating and the particle movement will be largely of
random nature. In case of low P�clet number we therefore expect to find a
locally homogeneous particle distribution. This shows that even if we do not
consider interparticle forces, the particle distribution is not known a priori.
There have been many approaches to calculate the average settling velocity of
the particles in a suspension. We will briefly describe Batchelor's idea [7]
which is based on two-particle interactions.
Batchelor considers a random suspension at low volume fraction
 .
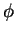He assumes that the particle distribution is homogeneous and calculates the pair
interaction between a test sphere positioned at
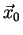and all possible positions of particles. The mean settling velocity is then
given by
 |
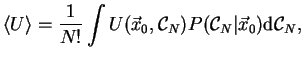(1.34) |
where
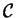is a configuration of
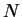spheres, and
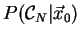is the conditional probability density of a configuration of
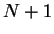particles given that there is a sphere at the position
.
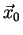The main problem is that the integral (1.34)
is divergent because the velocity field of a particle decays
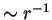 . He overcomes this
problem by calculating
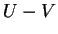where
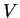is the translational velocity due to the nonuniform environment. In this
fashion, he finds
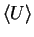up to order
,
 |
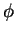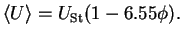(1.35) |
Although Eq. (1.35)
is only valid at low volume fractions, Batchelor's linear approximation of the
hindered settling function captures one of the main features of particle
suspensions. If the particle volume fraction is increased, the settling of the
particles is hindered due to the backflow of liquid caused by the other
particles.
For particle volume fractions larger than
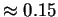the Eq. (1.35)
predicts negative settling velocities, i.e. the particles will rise. This shows
that the linear theory must not be applied over the whole range of possible
volume fractions. A second order approximation of the hindered settling function
would require to take three particle interactions into account. This approach
has been taken e.g. by P. Mazur et. al. and Brady et.al. [70,13]
and leads to better approximations of the hindered settling function. But in all
cases one has to make assumptions on the particle distribution within the
suspension.
The calculations of the hindered settling function assume that the particles
are distributed homogeneously within the volume. If this is not the case, say
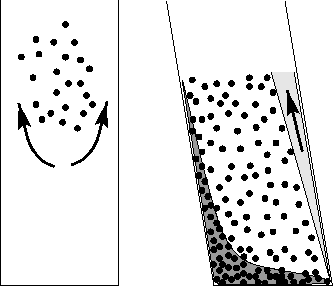
due to the initial conditions or generated by inclined walls as shown in Figure
1.1, the calculations are not valid any more. In case of inhomogeneous
initial conditions as shown on the left side of Figure
1.1, the backflow generated by the particles is not forced to move through
the particles but avoids the region of high particle concentration. Thus the
hindered settling effect is reduced. In the case of inclined walls, an initially
homogeneous distribution of particles will develop areas of higher
concentrations (dark grey in Figure
1.1) and areas of lower particle concentration (light grey), where the
upward moving fluid flows without the hindrance of settling particles.
Figure 1.1: Sketch of two situations where the
average particle settling velocity is increased due to a inhomogeneous
initial particle distribution (left side) or inclined walls (right
side). In both cases the backflow generated by the settling particles
avoids the particles and the average particle velocity is increased.
 |
A similar situation occurs when there are long-range interparticle forces or
other physical effects that lead to clustering of the particles. In such cases
the hindered settling function does not need to be a monotonically decreasing
function of the volume fraction.
|
