| What can you learn from the transfer function |
Where F(s) is any other rational polynomial function of s classical control texts call this a type 1system since 1/s is the laplace transform corresponding to integration you can think of this condition as a reqyurement for integrating the error signal e(t).
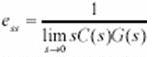
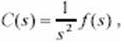if the error is
Where f(s) is any other rational polynomial function of s classical control texts call this a type 2 system since 1/s is the laplace transform corresponding to integration, you can think of this condition as a requirement for integrating the error signal , e(t), twice.
These arguments can be extended to specifications requiring the tracking of command signal with constant accelerations and even higher time derivatives.
4. Response of controlled systems to disturbance
A control system engineer�s life would be simple indeed if the only inputs to systems were the command signals, r(t). a more realistic view of a controlled system in the s-domain is shown below including:
- disturbance d(s) at the input to the plant
- disturbance D(s) at the output to the plant
- noise N(s) in the feedback loop
this system is linear so you can treat these disturbances as additional inputs and use superposition. To help
you use superposition correctly, you might consider breaking the feedback loop and an artificial �input� identical to the output 0(s), as show here
Two important facts are evident from these results:
- the denominators of all the transfer function terms are identical. Therefore so are the poles for all the
terms. Stability (or the lack of it) occurs under the same conditions for all the transfer functions
- As you change C(s) and or F(s) in order to design the control signal-output transfer function you want, these also affect the disturbance responses. Not surprisingly, design changes impose tradeoffs between the controller performance expressed in H(s) and the disturbance sensitivities S(s),S(s)and Sn(s).
5. frequency-domain models
By letting
S ?ja,
You can obtain the magnitude and phase of any of the transfer functions(s), S(s) and S(s), above. The control
engineer normally tries for the following frequency � domain characteristics in a designed system
- H : flat and as close to unity (0 dB) as possible from DC (0 Hz) out to as high a frequency as possible.
- |S (a) as small as possible in any frequency range where|D(a)| is
- | S (a) |: as small as possible in any frequency range where |D(a)is
- |Sn(a) |: as small as possible in any frequency range where |D(a)| is significant, for example if the main
output disturbance to a system that positions a large dish antenna is blowing wind, the disturbance spectrum ,|
aD(a) |, will be negligible at high frequencies and a large |S(a)|at high frequencies would have little effect on
system performance.
- |Sn(a)|: as small as possible in any frequency range where |N(a)|is significant.
Two important facts are evident from these results:
- the denominators of all the transfer function terms are identical. Therefore so are the poles for all the terms. Stability (or the lack of it) occurs under the same conditions for all the transfer functions
- As you change C(s) and or F(s) in order to design the control signal-output transfer function you want, these also affect the disturbance responses. Not surprisingly, design changes impose tradeoffs between the controller performance expressed in H(s) and the disturbance sensitivities S(s),S(s)and Sn(s).
|
