1. Fluid Dynamics
Objectives
- Introduce concepts necessary to analyse fluids in motion
- Identify differences between Steady/unsteady uniform/non-uniform
compressible/incompressible flow
- Demonstrate streamlines and stream tubes
- Introduce the Continuity principle through conservation of mass and
control volumes
- Derive the Bernoulli (energy) equation
- Demonstrate practical uses of the Bernoulli and continuity equation in
the analysis of flow
- Introduce the momentum equation for a fluid
- Demonstrate how the momentum equation and principle of conservation of
momentum is used to predict forces induced by flowing fluids
This section discusses the analysis of fluid in motion - fluid dynamics. The
motion of fluids can be predicted in the same way as the motion of solids are
predicted using the fundamental laws of physics together with the physical
properties of the fluid.
It is not difficult to envisage a very complex fluid flow. Spray behind a
car; waves on beaches; hurricanes and tornadoes or any other atmospheric
phenomenon are all example of highly complex fluid flows which can be analysed
with varying degrees of success (in some cases hardly at all!). There are many
common situations which are easily analysed.
2. Uniform Flow, Steady
Flow
It is possible - and useful - to classify the type of flow which is being
examined into small number of groups.
If we look at a fluid flowing under normal circumstances - a river for
example - the conditions at one point will vary from those at another point
(e.g. different velocity) we have non-uniform flow. If the conditions at one
point vary as time passes then we have unsteady flow.
Under some circumstances the flow will not be as changeable as this. He
following terms describe the states which are used to classify fluid flow:
- uniform flow: If the flow velocity is the same magnitude and
direction at every point in the fluid it is said to be uniform.
- non-uniform: If at a given instant, the velocity is not
the same at every point the flow is non-uniform. (In practice, by
this definition, every fluid that flows near a solid boundary will be
non-uniform - as the fluid at the boundary must take the speed of the
boundary, usually zero. However if the size and shape of the of the
cross-section of the stream of fluid is constant the flow is considered
uniform.)
- steady: A steady flow is one in which the conditions (velocity,
pressure and cross-section) may differ from point to point but DO NOT change
with time.
- unsteady: If at any point in the fluid, the conditions change
with time, the flow is described as unsteady. (In practise there is
always slight variations in velocity and pressure, but if the average values
are constant, the flow is considered steady.
Combining the above we can classify any flow in to one of four type:
- Steady uniform flow. Conditions do not change with position in
the stream or with time. An example is the flow of water in a pipe of
constant diameter at constant velocity.
- Steady non-uniform flow. Conditions change from point to point in
the stream but do not change with time. An example is flow in a tapering
pipe with constant velocity at the inlet - velocity will change as you move
along the length of the pipe toward the exit.
- Unsteady uniform flow. At a given instant in time the conditions
at every point are the same, but will change with time. An example is a pipe
of constant diameter connected to a pump pumping at a constant rate which is
then switched off.
- Unsteady non-uniform flow. Every condition of the flow may change
from point to point and with time at every point. For example waves in a
channel.
If you imaging the flow in each of the above classes you may imagine that one
class is more complex than another. And this is the case - steady uniform
flow is by far the most simple of the four. You will then be pleased to hear
that this course is restricted to only this class of flow. We will not be
encountering any non-uniform or unsteady effects in any of the examples (except
for one or two quasi-time dependent problems which can be treated at steady).
3. Compressible or
Incompressible
All fluids are compressible - even water - their density will change as
pressure changes. Under steady conditions, and provided that the changes in
pressure are small, it is usually possible to simplify analysis of the flow by
assuming it is incompressible and has constant density. As you will appreciate,
liquids are quite difficult to compress - so under most steady conditions they
are treated as incompressible. In some unsteady conditions very high pressure
differences can occur and it is necessary to take these into account - even for
liquids. Gasses, on the contrary, are very easily compressed, it is essential in
most cases to treat these as compressible, taking changes in pressure into
account.
4. Three-dimensional flow
Although in general all fluids flow three-dimensionally, with pressures and
velocities and other flow properties varying in all directions, in many cases
the greatest changes only occur in two directions or even only in one. In these
cases changes in the other direction can be effectively ignored making analysis
much more simple.
Flow is one dimensional if the flow parameters (such as velocity,
pressure, depth etc.) at a given instant in time only vary in the direction of
flow and not across the cross-section. The flow may be unsteady, in this case
the parameter vary in time but still not across the cross-section. An example of
one-dimensional flow is the flow in a pipe. Note that since flow must be zero at
the pipe wall - yet non-zero in the centre - there is a difference of parameters
across the cross-section. Should this be treated as two-dimensional flow?
Possibly - but it is only necessary if very high accuracy is required. A
correction factor is then usually applied.
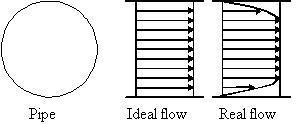
One dimensional flow in a pipe.
Flow is two-dimensional if it can be assumed that the flow parameters
vary in the direction of flow and in one direction at right angles to this
direction. Streamlines in two-dimensional flow are curved lines on a plane and
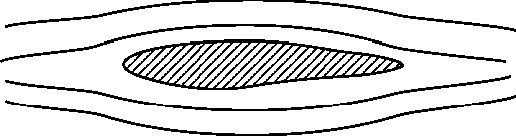
are the same on all parallel planes. An example is flow over a weir foe which
typical streamlines can be seen in the figure below. Over the majority of the
length of the weir the flow is the same - only at the two ends does it change
slightly. Here correction factors may be applied.

Two-dimensional flow over a weir.
In this course we will only be considering steady, incompressible one
and two-dimensional flow.
5. Streamlines and
streamtubes
In analysing fluid flow it is useful to visualise the flow pattern. This can
be done by drawing lines joining points of equal velocity - velocity contours.
These lines are know as streamlines. Here is a simple example of the
streamlines around a cross-section of an aircraft wing shaped body:
Streamlines around a wing shaped body
When fluid is flowing past a solid boundary, e.g. the surface of an aerofoil
or the wall of a pipe, fluid obviously does not flow into or out of the surface.
So very close to a boundary wall the flow direction must be parallel to the
boundary.
- Close to a solid boundary streamlines are parallel to that boundary
At all points the direction of the streamline is the direction of the fluid
velocity: this is how they are defined. Close to the wall the velocity is
parallel to the wall so the streamline is also parallel to the wall.
It is also important to recognise that the position of streamlines can change
with time - this is the case in unsteady flow. In steady flow, the position of
streamlines does not change.
Some things to know about streamlines
- Because the fluid is moving in the same direction as the streamlines,
fluid can not cross a streamline.
- Streamlines can not cross each other. If they were to cross this would
indicate two different velocities at the same point. This is not physically
possible.
- The above point implies that any particles of fluid starting on one
streamline will stay on that same streamline throughout the fluid.
A useful technique in fluid flow analysis is to consider only a part of the
total fluid in isolation from the rest. This can be done by imagining a tubular
surface formed by streamlines along which the fluid flows. This tubular surface
is known as a streamtube.
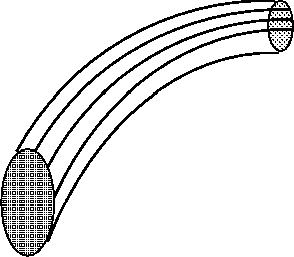
A Streamtube
And in a two-dimensional flow we have a streamtube which is flat (in the
plane of the paper):

A two dimensional version of the streamtubeThe "walls" of a
streamtube are made of streamlines. As we have seen above, fluid cannot flow
across a streamline, so fluid cannot cross a streamtube wall. The streamtube can
often be viewed as a solid walled pipe. A streamtube is not a pipe - it
differs in unsteady flow as the walls will move with time. And it differs
because the "wall" is moving with the fluid
|

