Similarity

1. Similarity

Hydraulic models may be either true or distorted models. True models reproduce features of the prototype but at a scale - that is they are geometrically similar.

2. Geometric similarity

Geometric similarity exists between model and prototype if the ratio of all corresponding dimensions in the model and prototype are equal.

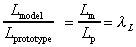
where l_L is the scale factor for length.

For area

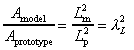
All corresponding angles are the same.

3. Kinematic similarity

Kinematic similarity is the similarity of time as well as geometry. It exists between model and prototype

1. If the paths of moving particles are geometrically similar
2. If the rations of the velocities of particles are similar

Some useful ratios are:

Velocity
 

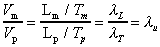
Acceleration
 

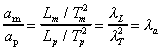
Discharge
 

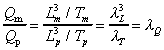
This has the consequence that streamline patterns are the same.

4. Dynamic similarity

Dynamic similarity exists between geometrically and kinematically similar systems if the ratios of all forces in the model and prototype are the same.

Force ratio
 

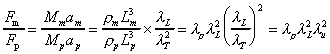
This occurs when the controlling dimensionless group on the right hand side of the defining equation is the same for model and prototype.
 

5. Models

When a hydraulic structure is build it undergoes some analysis in the design stage. Often the structures are too complex for simple mathematical analysis and a hydraulic model is build. Usually the model is less than full size but it may be greater. The real structure is known as the prototype. The model is usually built to an exact geometric scale of the prototype but in some cases - notably river model - this is not possible. Measurements can be taken from the model and a suitable scaling law applied to predict the values in the prototype.

To illustrate how these scaling laws can be obtained we will use the relationship for resistance of a body moving through a fluid.

The resistance, R, is dependent on the following physical properties:

r: ML^-3 u: LT^-1 l:(length) L m: ML^-1T^-1

So the defining equation is f (R, r, u, l, m ) = 0

Thus, m = 5, n = 3 so there are 5-3 = 2 p groups

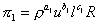
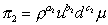
For the p₁ group

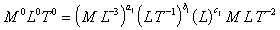
Leading to p₁ as

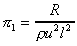
For the p₂ group

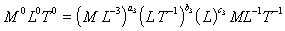
Leading to p₁ as

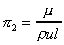
Notice how 1/p₂ is the Reynolds number. We can call this p_2a.

So the defining equation for resistance to motion is

f ( p₁ , p_2a ) = 0

We can write

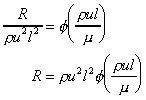
This equation applies whatever the size of the body i.e. it is applicable to a to the prototype and a geometrically similar model. Thus for the model

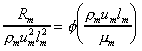
and for the prototype

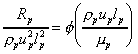
Dividing these two equations gives

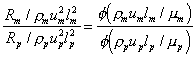
At this point we can go no further unless we make some assumptions. One common assumption is to assume that the Reynolds number is the same for both the model and prototype i.e.

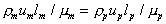
This assumption then allows the equation following to be written

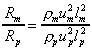
Which gives this scaling law for resistance force:

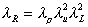
That the Reynolds numbers were the same was an essential assumption for this analysis. The consequence of this should be explained.

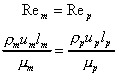
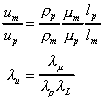
Substituting this into the scaling law for resistance gives

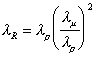
So the force on the prototype can be predicted from measurement of the force on the model. But only if the fluid in the model is moving with same Reynolds number as it would in the prototype. That is to say the R_p can be predicted by

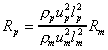
provided that

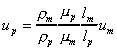
In this case the model and prototype are dynamically similar.

Formally this occurs when the controlling dimensionless group on the right hand side of the defining equation is the same for model and prototype. In this case the controlling dimensionless group is the Reynolds number.

6. Dynamically similar model examples

Example 1

An underwater missile, diameter 2m and length 10m is tested in a water tunnel to determine the forces acting on the real prototype. A 1/20^th scale model is to be used. If the maximum allowable speed of the prototype missile is 10 m/s, what should be the speed of the water in the tunnel to achieve dynamic similarity?
 

For dynamic similarity the Reynolds number of the model and prototype must be equal:

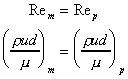
So the model velocity should be

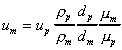
As both the model and prototype are in water then, m_m = m_p and r_m = r_p so

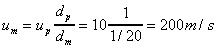
Note that this is a very high velocity. This is one reason why model tests are not always done at exactly equal Reynolds numbers. Some relaxation of the equivalence requirement is often acceptable when the Reynolds number is high. Using a wind tunnel may have been possible in this example. If this were the case then the appropriate values of the r and m ratios need to be used in the above equation.

Example 2

A model aeroplane is built at 1/10 scale and is to be tested in a wind tunnel operating at a pressure of 20 times atmospheric. The aeroplane will fly at 500km/h. At what speed should the wind tunnel operate to give dynamic similarity between the model and prototype? If the drag measure on the model is 337.5 N what will be the drag on the plane?

From earlier we derived the equation for resistance on a body moving through air:

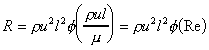
For dynamic similarity Re_m = Re_p, so

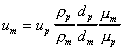
The value of m does not change much with pressure so m_m = m_p

The equation of state for an ideal gas is p = rRT . As temperature is the same then the density of the air in the model can be obtained from

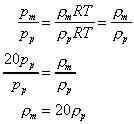
So the model velocity is found to be

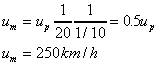
The ratio of forces is found from

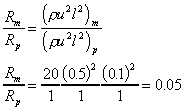
So the drag force on the prototype will be

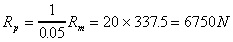
7. Models with free surfaces - rivers, estuaries etc.

When modelling rivers and other fluid with free surfaces the effect of gravity becomes important and the major governing non-dimensional number becomes the Froude (Fn) number. The resistance to motion formula above would then be derived with g as an extra dependent variables to give an extra p group. So the defining equation is:

f (R, r, u, l, m, g ) = 0

From which dimensional analysis gives:

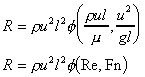
Generally the prototype will have a very large Reynolds number, in which case slight variation in Re causes little effect on the behaviour of the problem. Unfortunately models are sometimes so small and the Reynolds numbers are large and the viscous effects take effect. This situation should be avoided to achieve correct results. Solutions to this problem would be to increase the size of the model - or more difficult - to change the fluid (i.e. change the viscosity of the fluid) to reduce the Re.

8. Geometric distortion in river models

When river and estuary models are to be built, considerable problems must be addressed. It is very difficult to choose a suitable scale for the model and to keep geometric similarity. A model which has a suitable depth of flow will often be far to big - take up too much floor space. Reducing the size and retaining geometric similarity can give tiny depth where viscous force come into play. These result in the following problems:

1. accurate depths and depth changes become very difficult to measure;
2. the bed roughness of the channel becomes impracticably small;
3. laminar flow may result - (turbulent flow is normal in river hydraulics.)

The solution often adopted to overcome these problems is to abandon strict geometric similarity by having different scales in the horizontal and the vertical. Typical scales are 1/100 in the vertical and between 1/200 and 1/500 in the horizontal. Good overall flow patterns and discharge characteristics can be produced by this technique, however local detail of flow is not well modelled.

In these model the Froude number (u²/d) is used as the dominant non-dimensional number. Equivalence in Froude numbers can be achieved between model and prototype even for distorted models. To address the roughness problem artificially high surface roughness of wire mesh or small blocks is usually used.