Structural Engineering
Structural Engineering Activities
Structural engineering is mainly involved with two activities
- 1. Structural Analysis
- 2. Structural Design
Structural Analysis
It deals with analysing a particular structural system. A structural system
may vary from simple systems (like beams, columns, slabs, etc) to more complex
systems (like frames, bridges, piers, foundations, retaining walls, etc). The
objective behind analysis is to estimate or find resultant stresses (or forces)
so that these elements can be designed to withstand the load that comes over it.
Analysis of Statically Determinate Structures
Idealized Structures
In reality the exact analysis of a structure can never be carried out.
Idealizing a structure is a method of conservatively simplifying the components
of the structural system, while keeping its behavior under loading the same.
This is done in order to simplify calculations. Without an idealized structure,
design could take a massively longer amount of time... and sometimes becomes
impossible. It is important for a structual engineer to develop methods to
idealize a structure in order to carry out analysis.
Supports for Coplanar Structures
Structural Members are joined together by supports depending on the intent of
the engineer. Three types of joints most often used are pin connections, roller
supports, and fixed joints. Pin connections provide vertical and lateral
support, but cannot provide a moment reaction. A roller support can only supply
a reaction of a force in one direction. A fixed joint provides vertical, lateral
as well as a moment reaction.
Analysis of Statically Determinate Trusses
Typically done using method of joints, or method of sections.
Internal Loadings Developed in Structural Members
Internal loadings are found by "cutting" the member and applying the
equations of equilibrium.
Cables and Arches
What are cables and arches?
Influence Lines for Statically Determinate Structures
Influence lines are a diagram that represents variation of a loading function
at one location on a structure. For example, a truck drives across a bridge:
When the truck is at the left side on top of the bridge, very little loading
is felt at the right support. The function represented by influence lines
changes as the truck moves towards the right end of the bridge. The loading at
the right support grows as the truck nears it, until the truck reaches the far
end, where the end realizes the maximum loading. Influence lines for statically
determinate structures consist of a straight line.
Deflections
Deflections occur naturally in structures from various sources. Loads and
temperature changes are sources of deflections that structural engineers have to
design for because they are unavoidable. Designs must be made in order to avoid
cracking of the materials used. Fabrication or Design Errors can lead to failure
of structures and should be avoided through careful planning and analysis.
Structures in most cases are built with materials that can withstand the
designed loading and only have a linear elastic response. Under these conditions
loads may cause deflections, but when the load is removed the structure will
return to it original shape and strength. Overloading beyond the linear elastic
response may cause damage and failure of the structure. This is referred to as
"plastic deformation".
Elastic-Beam Theory
If a material is homogeneous and behaves in a linear elastic manner we can
derive a nonlinear second order differential equation that when solved through
the double integration method can give a solution deflection as a function of x.
We must assume dv / dx = 0 relative
to the length of the beam in the x-axial direction.
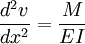
M = the internal moment in the beam E = the material's modulus of elasticity
I = the beam's moment of inertia computed about the neutral axis v = deflection
The Double Integration Method
When Moment can be expressed as a function of position x, then performing
double integration will yield the beam's slope as a function of x, and the
equation of the elastic curve.
The two integrations will yield two constants of intergration. Using the
boundary conditions the constants can be solved for.
Castigliano's theorems
First theorem
- If the strain energy of an elastic structure can be expressed as a
function of generalised displacement qi; then the partial derivative of the
strain energy with respect to generalised displacement gives the generalised
force Qi.
Using this theorem the generalised forces acting on the structure can be
calculated.
Second theorem
- If the strain energy of a linearly elastic structure can be expressed
as a function of generalised force Qi; then the partial derivative of the
strain energy with respect to generalised force gives the generalised
displacement qi in the direction of Qi.
Using this theorem the generalised displacement of the structure can be
calculated. Castigliano's method usually refers to the application of his
second theorem.
Structural Design
Structural design is the process of selecting members of required dimensions
such that they provide adequate stability under service loads. There are two
conditions that a structural designer must keep in mind. One is "stability" and
the other is "serviceability". Stability of a structure means that it can resist
the loads acting on it satisfactorily and that the structure will not collapse
immediately (that is, it provides enough time to escape to safety).
Serviceability refers to certain conditions that are required so that the
structure remains serviceable. For example, consider a bridge that can resist
service loads without collapse. This is a "stable" structure. Now assume that
this bridge shows abnormal deflections. The deflections could be such that the
bridge feels bouncy and could lead to steering problems for vehicles crossing it
at high speeds. As such this may not cause the structure to collapse. So we can
say that the structure is stable, but according to serviceability criterion it
is not serviceable because people could feel afraid of using the bridge.
In the design and construction of the foundation and framing for buildings
and bridges, the main materials used are concrete, steel, timber, and masonry.
Steel can further be subdivided into two subsections: hot-rolled steel and and
cold-formed steel. Cold-formed steel applies to material of approximately 1/8"
or less in thickness that is either folded or roll-formed from flat sheets into
structural shapes while at room temperature.
Safety Factors
All structures must be designed to carry all foreseeable loads with a
suitable factor of safety. Clearly it would be unsafe to walk on a structure
that was adequate but had no margin of safety built in. With this in mind, most
countries have standards that prescribe the required minimum safety factors for
structures. The minimum is usually a factor of about 1.7. This is not a factor
to allow for overloading or poor workmanship. If there is a possibility of
overloading or poor workmanship, the design loads must be increased to account
for the overloading and the strengths of the materials upon which the design is
based must be reduced to account for the poor workmanship. The safety factor
must remain complete, as it is there to account for the unexpected events and
unforeseen circumstances. If a structure becomes worn, loose, cracked or
corroded, it should always be repaired so the safety factor is preserved.
|

