Now consider what happens when a current source is connected to a node.  You might suspect that this situation is the most complex of all, but, in fact, it is one of the simpler ones.  In the example below the current source is deliberately set so that the current is actually flowing into the node if I_s is positive.  Now, consider writing the current equations for this circuit.

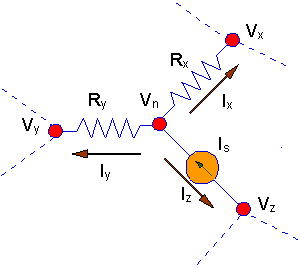
I_x +I_y + I_z = 0

becomes:

        Given all of the above, there is one last question.  That is, "How many independent equations result when KCL is written at all of the nodes?",  Consider the following:

• Assume that the circuit is composed of resistors, voltage sources and current sources.  Assume that the circuit hasn + 1 nodes.
• One of the nodes in the circuit must be chosen as areference.  Usually, if there is anode connected to ground, then that will be the reference.
  • Otherwise, choose any other node as the reference.
• All other node voltages will be measured from the voltage at the reference node.  That reduces the number of voltages that must be found from n + 1 to n.
• Every other node voltage is potentially an unknown voltage that must be found - n node voltages in all.
• If there is a grounded voltage source, then one node voltage is determined by that voltage source - at the ungrounded end of the voltage source.
  • Every grounded voltage source reduces the number of unknown node voltages by one.  If there aren_Vg grounded voltage sources, that reduces the number of unknown node voltages byn_Vg ton - n_Vg.
• If there are ungrounded voltage sources, then those ungrounded sources fix the difference in voltage between two nodes.  Essentially, if you know one of those node voltages, you can compute the other.  Thus, each ungrounded voltage source also reduces the number of unknown node voltages by one.
• If there are current sources in the network, theyhave no effect on the number of unknown node voltages, although it will most definitely have an effect on the value of node voltages in the network.
• Thus, the number of node equations isn - n_V, wheren_V is the number of voltage sources in the network.
• You get those equations by writing KCL at every node not connected to a voltage source (grounded or ungrounded) and one of the nodes connected to every ungrounded voltage source.

        After writing the node equations, the next problem is to put them in a form that is easier to solve, and that is the next thing you have to consider.

---

Getting A Set Of Simultaneous Equations

        Once the KCL equations are written for a network, the next step is to cast the equations into a form amenable to solution.  The form you should be looking for is a set of simultaneous linear equations.  In other words, you are looking for something like the following:

a*x + b*y + c*z = j

d*x + e*y + f*z = k

g*x + h* y + i*z = l

This is a standard form for simultaneous linear equations, and for circuit equations the variables (x, y and z) would probably be node voltages (e.g. V_x, V_y and V_z).

        Considere a typical node voltage equation (taken from earlier in this lesson):

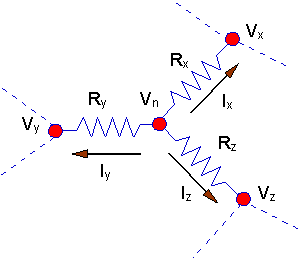
(V_n -V_x)/R_x + (V_n -V_y)/R_y + (V_n -V_z)/R_z = 0

Separate all of the terms that involve V_x, etc. and combine, and the result is:

(1/R_x + 1/R_y + 1/R_z)V_n - V_x/R_x - V_y/R_y  - V_z/R_z = 0

And this is the form we want.  This particular equation has four unknown node voltages, but that would be the case for the node shown just above.

        Similar equations occur for the other possibilities.

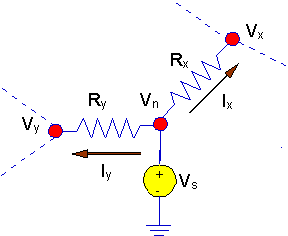
If there is a grounded voltage source, no KCL equation is written at that node because the node voltage is known:

V_n = V_s

If there is an ungrounded voltage source, there is one less KCL equation.

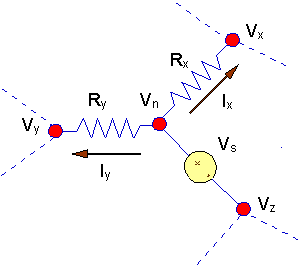Here there are two possibilities.

We could write:

V_n = V_s + V_z

Then we would write a KCL equation at node "z" that included I_x and I_y flowing away from node "z'.  Here is an example to illustrate the point.

---

Example  

E1   In this circuit, note the following:

• The voltage at node "x" is known:
  • V_x = V₁

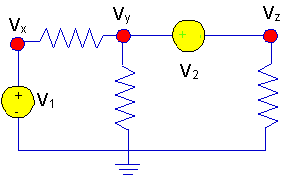
• We can select either node "y" or node "z" as the node with the unknown voltage.  Select one, and the other is determined.  We will take V_y as the unknown voltage, so:
  • V_y = V_z + V₂
• We can write KCL at node "y".  Actually, it may be better to think of a supernode that includes both node "y" and node "z".  The green shading shows the supernode.  The sum of the currents leaving the supernode must sum to zero - for the same reason that the sum of the currents leaving a node sum to zero - conservation of charge!

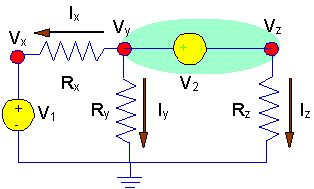        Write the KCL equations for the entire super node: I_x + I_y + I_z = 0 Then, note that: I_x = (V_y -V_x)/R_x

I_y = V_y / R_y

I_z = V_z / R_z= (V_y - V₂)/ R_z

And the KCL equation for the supernode becomes:

(V_y -V_x)/R_x + V_y / R_y + (V_y - V₂)/ R_z = 0

And, for this circuit that is the one independent KCL equation that can be written (unless you choose to keep V_z as your unknown, but there is still only one equation.)  That means writing this in the standard form, we would have:

(1/R_x + 1 / R_y + 1/ R_z)V_y  - V_x/R_x = V₂/ R_z

The coefficient of V_y is the sum of the conductances connected to the supernode, the source appears on the right hand side, and the negative reciprocal of the shared resistor shows up just where we might expect it.