| Power & Energy |
Power In Batteries
Batteries are ubiquitous components. They are in TV remotes, cell phones
and things like that. But, batteries also appear in places you don't
expect them to be. For example, you can turn this computer off. When
you turn it back on it remembers things and recalculates things like the time.
Now, you expect that for things that can be stored on a hard drive. You
don't expect it for the time.
When you turn this computer off and later turn it back on it will have the
right date and time. How does it do that? If you think about it
(and don't do that for too long!) you have to believe that there is a
battery somewhere inside the computer and that when you turn the computer
off that battery runs some sort of little clock hidden inside the computer.
You can't see the clock and you wouldn't even know it's there, but you can
probably see the time now on the task bar of this computer - and it's
probably close to being right!
Batteries are used to solve many problems.
-
They are used to provide power
to run things like computer clocks that need to keep running even in the absence
of AC power.
-
They are used to store energy
for things like starting a car. When you run the car you generate energy
(from the gasoline) and store it in the car battery. Then there is energy
there when you need it to get the car going again.
-
They are used for low power
devices to make them portable. That includes things like cell phones, TV
remotes and calculators.
You use batteries - whether you want to or not, and whether you know it or
not! You need to be able to compute some of the quantities involved.
Here is a simple circuit where a resistor is connected to a battery.
We know some salient facts about this circuit.
-
There is energy stored in the
battery and the battery delivers stored energy to the resistor.
-
The resistor dissipates energy,
and what happens physically is that the electrical energy that is delivered to
the resistor gets turned into heat energy and the resistor becomes warmer.
Now, we need to look at a circuit diagram for this situation. That
circuit diagram is shown to the right of the picture below.
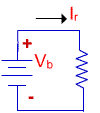
-
In the diagram, we have defined
a battery voltage, Vb ,
and a current, Ir.
-
Notice that we have used a
natural definition for the current polarity. We have the arrow pointing
out of the battery and into the resistor. We do that because we know that
positive charge actually flows from the battery terminal through the resistor.
-
That definition of current
polarity raises questions about calculation of power to/from the battery. Let us
consider the power flow into the battery. 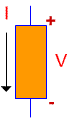
Power flow into the battery
or any other device - is the product, VI, when
-
V
is the voltage across the device, and
-
I
is the current flowing into the device.
-
Remember, for our polarity
conventions here, the current arrow points into the terminal of the device that
is labelled "+" for the voltage definition.
We have reproduced the diagram from above here to emphasize how the voltage
and current polarities are defined. Notice that the current arrow in
our earlier definition points toward the "+" sign on the device.

In the battery-resistor circuit below, the current arrow is directed out of the
positive ("+") terminal of the battery. That means the power delivered to
the battery must be computed by (note the minus sign!):
P = - VI
What does this mean?
Let's look at a numerical example. Let's assume the battery voltage is 12
volts and the resistor is 24 ohms. That means the current is 0.5 amps,
i.e.:
Ir = 12v/24W
= 0.5a
In other words, the power
flowing into the battery is:
P = - Vb
Ir = - 12 * 0.5 = - 6w
-
The power flowing into the
battery is negative!
-
The power flowing out of the
battery is positive!
-
And, it makes sense because we
know the battery supplies power. How much energy is stored in a
battery?
-
Batteries are often rated in
ampere-hours (or milliampere-hours) and an ampere-hour is really a unit of
charge.
-
As a battery is used it
discharges - charge flows from the battery - but it tends to hold a constant
voltage. This is different than the internal resistance of the battery.
What we are saying here is that as time goes on - for the same current drawn
from the battery - the voltage stays about the same. There may be a slight
drop-off but it is not very large.
-
Thus, if we have a 12.6 v
battery, it will have something close to 12.6v until it gets close to being
discharged.
-
Let's say we have a 12.6v
battery rated at 70 ampere-hours.
-
Assuming it can deliver 1
ampere for 70 hours, then it will be delivering
-
Power = 12.6v x 1.0 amp = 12.6
watts for 70 hours.
-
That works out to 12.6 x 70 =
882 watt hours or .882 kw-hr. - and remember you pay the
-
electric company by the
kilowatt-hour!
-
In joules we have 882 w-hr x
3600sec/hr = 3,175,200 joules.
That might sound like a lot, but an interested student might want to compare
that amount of energy with the energy stored in a gallon of gasoline. |

