Average
Let's
examine another aspect of a signal that is often important. Signals
can have an average value. The average
value - denoted by Vavg here - is given by:

Let's look at an example - the signal we
saw earlier.
Example
If we have a signal that is represented by:
V(t) = 2 + 12sin(2p500t)
This is a periodic signal, and we can compute
the average of this signal. Since the average involves an integral
over one period of the periodic signal, we are free to choose where the
interval starts. In this example, the simplest thing is to integrate
from t = 0 to t= T, noticing that the signal repeats 500 times a second
so the period is .002sec.
Doing the integration, we have:
 We will leave the details to you. In particular:
We will leave the details to you. In particular:
-
The integral of the sine
- over a single full period - is zero.
-
Check it by doing the
integration.
-
Consider a sine wave plot
for a single full period, and notice that the area above the axis is the
same as the area below the axis. Remember, it's just the sine wave,
and it doesn't include the 2.
-
The integral of the constant
part becomes:
-
(1/T)*(2T) = 2
-
So, the average of 2 is
2. Seems right.
The net result is that the average of this signal
is simply 2v. Note the following.
-
Sinusoidal signals have
no average value.
-
Constant terms have an
average value equal to their value.
-
The average value is very
often referred to as the DC Component
of the signal.
RMS
Voltage
RMS voltage is a more sophisticated concept - even though it is a concept
that has a longer history than most electrical concepts.
When AC and DC power distribution systems were both in existence, there
was a need for some standardization between the two different systems.
If you bought a 100 watt light bulb it would only consume 100 watts if
the voltages were the same. But, how do you measure AC voltage in
a way that assures that it will work to produce the same amount of light
as the same DC voltage? After all, the AC voltage is changing value
all of the time, so you can't way what voltage it is because it's going
to change. That won't help you with your light bulb. What was
needed was a measure of AC voltage that allowed you to use the AC voltage
value the same way you used the DC voltage value when you computed power.
The problem here is that power is computed as V2/R.
If you have 100 volts and you have a DC voltage there's no problem.
If you have an AC voltage you might have a signal that looks like this
one.
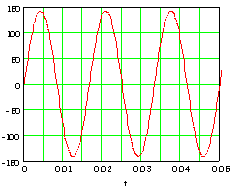
Is this AC voltage 100 v? Well, actually, sometimes it is much bigger
than 100v, and it looks like the positive peak is around +140 v and the
negative peak is around -140 v. That means that sometimes it is much
larger than 100v. However, there are other times when the voltage
is much less than 100v, and it even passes through 0v every so often!
It begins to look like you can't say what this voltage is because it changes
constantly.
Now, let's think about that light bulb again. In a light bulb, the
thing that determines the amount of light is the power that is put into
the filament. It's the power that we need to be concerned about.
In the early days of electricity, one of
the first products to become widely used was the incandescent light bulb.
In the light bulb, the amount of light produced depends upon the temperature
of the filament, which in turn depends upon the power dissipated as heat.
Also, you don't get the perception that the light bulb lights up and goes
off 120 times a second. (The signal above has a peak - either positive
or negative - 120 times a second because it is a 60 Hz. signal.)
When the voltage goes through zero and the power goes to zero when the
voltage goes to zero. Even though the power goes to zero, the light
bulb does not heat up or cool off instantaneously. What really counts
in the light bulb is average power. Let's compute the average power.
We'll do that by assuming that the voltage appears across a resistor, R.
-
First, note that the instantaneous
power is v2(t)/R.
-
Second, note that we can
then compute the average power. To get the average power we must
compute the value of the integral below - which is not difficult to get
to once you have computed the average above.

Now, let's look at the evaluation of this
integral. We can substitute a general expression for the voltage
as a function of time. Here is the result.
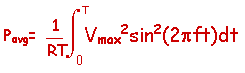
The easiest way to evaluate this integral
is to expand the squared-sine function.

Now, we know that the cosine function (at
twice the frequency) will have no net area, and the integral becomes:
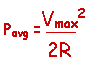
Now, if we had a DC voltage, V, the power
in a resistor, R, would be V2/R. If we wanted to
adjust the voltage, V, so that it produced the same average power as the
AC voltage (and call that value that produces the same average power Veq),
we would have to have.
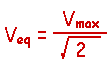
Actually, this value of voltage is only sometimes
called the equivalent voltage. If you trace the derivation backwards
you will see that the equivalent voltage is the root (the square root)
of the mean (i.e. the average) of the square (the square of the voltage
as a function of time). It's usually called the RMS (for Root-Mean-Square)
voltage. That's why we gave that title to this section after all.
Example
We all know that the AC line voltage is 115 volts or thereabouts.
What that means is that the RMS voltage is 115 volts. If you wanted
to write a time function for the voltage we would write:
V(t) = 162.6sin(2p60t
+ f)
Where did we get 162.6? We got that
by multiplying 115 by the square root of 2. And, we included an arbitrary
phase angle when we wrote the function.
Problems
Here is a sinusoidal signal. Willy Nilly has measured this signal,
and acquired it in a computer file and plotted it for you. Determine
the amplitude of this signal.

| 
