Frequency
of Sinusoidal Signals
Frequency is a parameter that determines how often the sinusoidal signal
goes through a cycle. It is usually represented with the symbol f,
and it has the units hertz (sec-1 ). Here is the
simulator you saw above.
This signal repeats every 4 seconds.
We say that this signal has a period of 4 seconds, and we usually represent
the period of the signal as "T". Here we have T = 4 sec. The
frequency of the signal is the reciprocal of the period. That's why
the frequency is indicated as 0.25 in the simulator. When "f" is
the frequency, we have:
f = 1/T
f is in Hertz (Hz)
T is in seconds (sec)
For the signal above, the frequency is 0.25
Hz. We get that from:
f = 1/T = 1/2 = 0.25
Hz.
Now, you can also change
the frequency in the simulator above. Change the frequency and observe
what happens. Try a frequency of 0.5 Hz, 1 Hz, etc.
Problem
P2.
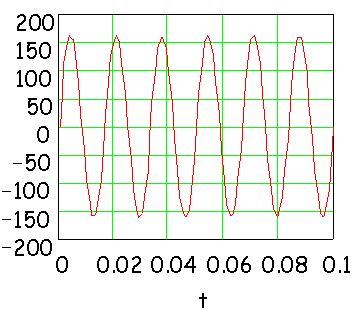
Here is Willy Nilly's signal again. Determine the frequency of this
signal. Hint: First determine the period of the signal.
|