A/D Converters
Analog-to-Digital converters - a.k.a. A/D
converters - are widely used by many engineers and scientists of all types,
often without their realizing it. Whenever they make a measurement of a
voltage, and that measurement is taken into a computer, an A/D is used.
If you're going to take measurements - and
just about every engineer will do a lot of that - then you will be better off if
you understand some of the basic ideas behind A/D converters. There are two
simple goals for this lesson.
 Given an A/D converter with a given range and number of bits,
Given an A/D converter with a given range and number of bits,

To be able to calculate the resolution of the converter.
 Given an A/D converter in the laboratory,
Given an A/D converter in the laboratory,

To be able to determine the resolution of the converter and the number
of bits used in the converter.
What Are A/D Converters?
A/D converters are electrical circuits
that have the following characteristics.
The input to the A/D
converter is a voltage.
A/D converters may be
designed for voltages from 0 to 10v, from -5 to +5v, etc., but they
almost always take a voltage input. (Some rare exceptions occur with
current inputs!) In any event, the input is an analog voltage signal
for most cases.
The output of the A/D
converter is a binary signal, and that binary signal encodes the analog
input voltage. So, the output is some sort of digital number.
A comparator can be used as a simple one-bit
A/D converter. Although a converter with just one bit isn't particularly
useful, you can begin to see how an A/D converter works by puttering with it for
a moment. If you read the lesson on comparators you encountered a simluation of
a comparator. That simulator is reproduced below.
Comparator Simulator
Sim1
Here is the comparator simulator. You can think of a
comparator as a one-bit A/D converter. The input is an analog signal, and the
output is a one bit digital representation of the analog signal. In the
simulator, you can control a simulated voltage source that is the input the the
comparator, and the digital output bit is indicated with a simulated LED.
Notice the following.
The input can range from zero
(0) to ten (10) volts. When the input voltage goes
above five (5) volts, the output is a binary one (1) and the LED lights.
When the input voltage is less than five volts, the output is a binary zero
(0) and the LED does not light.
Properties of A/D Converters
The comparator simulation reveals a few
important facts about A/D converters.
An A/D converter has a
range. The simulator has a range from 0v to 10v, or a total of ten (10)
volts. The total range of an A/D is the difference between the highest and
lowest voltages the A/D can convert. An A/D has a resolution that
is determined by the largest count that the A/D's counter/register can hold. The largest count is
determined by the number of bits in the counter.
If there are N bits in
the counter, the largest count is 2N-1. In the comparator, there
is only one bit, and the largest count is 1, and there are only two
different outputs that are possible.
Clearly, if you want a more accurate
conversion the converter will need to have a lot more than just one bit. Let's
look at another simulation. This simulation is a four-bit A/D converter.
Now, consider the following observations about the converter above.
There are four bits in the
simulation converter. The range is from 0v to 10v,
or 10v total range. With four bits, there are 16
different count values (0 through 15). Thus, 10v is divided into 16
different parts, each part being:
Now, let's consider an example question.
Example
E1
How many bits would you need to divide 10 v into .01 v
intervals? To get the answer to the question consider the following.
If you divide 10 v into .01 v
intervals you need 1000 intervals. If you need 1000 intervals
you need to think about a power of 2 that is larger than 1000.
That means that you need 10
bits in the converter, and the the count in the counter/register will run
from 0 to 1023. And that leads us to observe
that real converters often go to 10.23v, not 10v because that gives perfect
.01v increments between resolvable voltages.
Almost all A/D converters
use a scheme in which the analog voltage is first converted into a binary
integer (a "count", as in the simulator above) when the conversion is done. In
some cases, there may be some software that gives you the actual count - the
binary integer. In other cases the conversion might be converted - using
software - to a a numerical value or a character representation of a numerical
value.
Example
E2
A GPIB (IEEE-488) voltmeter is used to measure a DC
voltage. The instrument uses an A/D converter that generates a binary number.
Within the instrument, that binary number is converted to a string of characters
which is, in turn, transmitted to a computer connected to the instrument.
To illustrate the concept in the example,
consider the revised simulator below. In this simulator, the conversion
algorithm - from the count in the register to an analog voltage - is given by:
Of course, the simulation
only raises a few more issues.
Using this expression for the calculated
voltage, we can plot the calculated voltage as a function of the count. That's
shown in the figure below.
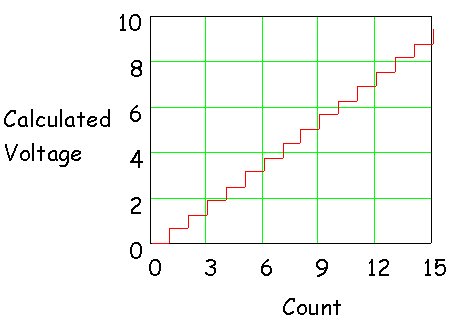
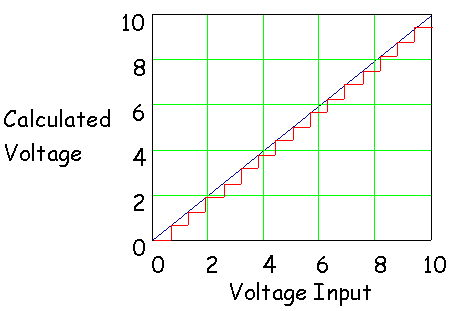
Even more interesting is the plot of the
calculated voltage against the voltage input that is being measured. That's
shown next. We've also included a plot (the blue line) that shows what the
output would be ideally (And that might take many, many bits in the
converter!). Notice that the calculated voltage is always lower than the
voltage input using the calculation method we assumed above. Note also that the
largest error occurs just before the converter switches when the voltage is
rising. For example, as the voltage rises from 0v to 3v, there is a time when
the converter output switches from 0v to 0.625v. The largest error occurs just
before that point, so a bound on the error is:
Error < 0.625
We can reduce the error if we calculate
the voltage differently. We can examine what happens if we use a different
expression for the computed voltage. We will use:
The result is shown in the next simulator.
Now, here is a plot of the calculated voltage
against the voltage input that is measured. Notice that the error limit is half
of what it was using the first calculation method.
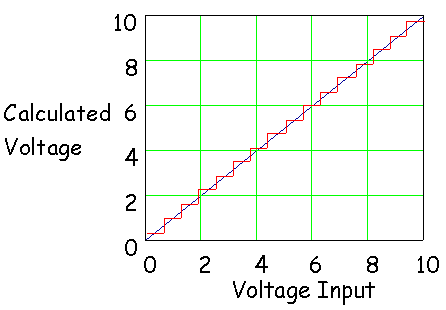
The conclusion is that the way the voltage
is computed can affect the average error when an A/D is used to measure voltage
values.
Whenever you buy an A/D converter, or a
voltmeter, or a data acquisition unit, you need to be cognizant of how the data
presented to the user is actually computed. That's not usually a problem in
instruments, but there are A/D computer cards that use the first method above to
calculate voltage, and you should be aware of that when it happens. It is less
important when the number of bits in the converter is higher, but when you have
high requirements for accuracty you should be thinking of what might be taking
place.
|

