Why Interface Circuits?
Computers don't exist in a vacuum. They
have to interface with the world in many ways. You can sit at a keyboard and
type and you're using a computer interface. You click a mouse button and that's
another interface. Measurement devices often need to communicate with computers
also.
There are numerous other situations where you
need to have a computer produce a specific voltage for some purpose.
Goals
Here's what you should be able to do after
this lesson.
A Simple Digital To Analog Converter
We are going to start by examining a
simple circuit. This circuit is an operational amplifier circuit with three
input voltages.
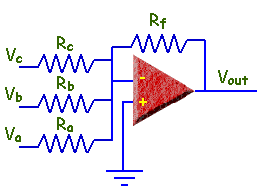
Each input voltage is either
zero volts or five volts and represents a logical 0 or 1. The input resistors are
chosen so that they are not all equal. The resistors are related
by: Rc = 2Rb = 4Ra.
To understand how this circuit works we will
need to obtain a symbolic expression for the output voltage - one in which we
express the output voltage in terms of the binary number that the input
represents. We already have an expression for the output voltage.
Vout = (RfVa
/Ra) + (RfVb /Rb)
+ (RfVc /Rc)
We need to interpret this output voltage
expression when the inputs represent a binary number.
Let's examine the expression for the
output voltage using the relation we required for the resistors.
Rc = 2Rb
= 4Ra
Then, the output voltage expression becomes:
Vout = (RfVa
/Ra) + (RfVb /Rb)
+ (RfVc /Rc)
Vout = (RfVa
/Ra) + (RfVb /2Ra)
+ (RfVc /4Ra)
Each input voltage is either zero (0) or
five (5) volts, representing either a zero or a one. Although we shouldn't mix
Boolean algebra variables and ordinary algebraic variables, we are going to.
We're going to say
Va = 5A2
Vb = 5A1
Vc = 5Ao
So
Vout = (Rf/4Ra)(4Va
+ 2Vb + Vc )
Vout = (5Rf/4Ra)(4A2
+ 2A1 + Ao )
And, the question we
are left with is "What is (4A2 +
2A1 + Ao )?"
The expression - (4A2
+ 2A1 + Ao ) - can be regarded as the binary
number represented by A2, A1 and Ao.
This table shows the equivalence.
A2
|
A1
|
Ao
|
Binary #
|
4A2+2A1+Ao
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
2
|
2
|
0
|
1
|
1
|
3
|
3
|
1
|
0
|
0
|
4
|
4
|
1
|
0
|
1
|
5
|
5
|
1
|
1
|
0
|
6
|
6
|
1
|
1
|
1
|
7
|
7
|
In other words, A2
is the 4 bit, A1 is the 2 bit and Ao is the
1 bit.
After all this, we reach
these conclusions for this circuit.
The inputs can be thought of
as a binary number, one that can run from zero (0) to seven (7). The output is a voltage that
is proportional to the binary number input. The circuit itself converts a
digital representation of a number to an analog version of the same number.
The circuit is a digital-to-analog converter also known as a D/A converter.
What if we wanted to convert
a digital signal with more bits? The answer to this question should be fairly
obvious.
More input resistances are
needed. The resistances should be
chosen in ratios of 2. The LSB has the largest
resistance. More significant bits have
resistances that decrease by a factor of 2.
Next, we're going to look at
some circuits that use the D/A converter.
One application of a D/A
converter is to convert signals generated within a computer to voltages
outside the computer. Examples where this is useful include control
systems, where a control signal could be calculated by a computer
(implementing some known control algorithm) and then converted to a voltage
using a D/A converter. That voltage could end up driving a motor for a pump
- among many other things that might occur. D/A converters also occur
within larger systems. Shown below is an example.
A pulse generator
generates a pulse train - a sequence of zeros and ones. The pulse train is
counted by a counter. The counter output is the
input to the D/A. The D/A output is
compared to the voltage input, and when the D/A output exceeds the
voltage input, the comparator output changes state and stops the
counter.
The second example is really
an A/D converter. It's interesting that many A/D converters contain D/A
converters within them. D/A converters are often emedded in places where you
might not expect to find them. You use them all the time.
You may not think that you
have ever used a D/A, but we will convince you that you have. We'll do that by
having you use one you have used before.
First, we need a source of
digital signals that we can convert to analog signals. The most common source
like that is a music CD. Consider what happens when you play a music CD.
(Note, we're deliberately emphasizing the phrase music CD because we want to
emphasize it is not a CD with program files on it that we want to use.)
Your CD has tiny little pits
on the surface. You can't really see them, but they are there. A low power laser is flashed
on the CD, and the reflectivity is different where there is a pit. That
means that the reflected laser signal can be used to read the zeroes and
ones on the CD. So, as the CD spins in the
holder, a sequences of zeroes and ones is generated and sent on. That sequence of zeroes and
ones is converted to an analog voltage that is amplified and fed to an
earphone or a speaker. So, you see that you have
used an A/D before - if you have ever used a CD player.
|

