Digital Signals and Logic Circuits

Flip-Flops

Why Study Flip-Flops?

There are some circuits that are not quite as straight forward as the gate circuits we have discussed in earlier lessons. However, you still need to learn about circuits that can store and remember information. They're the kind of circuits that are used in computers to store program information - RAM memory.

In this lesson we'll look at the background for those kinds of memory circuits. Our goal is the following.

Given a flip-flop circuit,

Determine how the circuit will behave for a sequence of inputs.
Be able to use a flip-flop to store a single bit.

Basic Circuit

Here's a basic circuit that involves just two NAND gates. There are two inputs to this circuit, X and Y. Can you generate a truth table for this circuit?

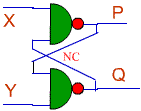
• Note that there is no connection where the two wires running from the output back to the input cross.

Let's review what you know about this circuit. We can focus on what happens when X= 0, and Y = 0, the first entry in the truth table above.

• If X = 0, then P = 1. We know that if either input to a NAND gate is 0, the output is 1.
• Now. try to take advantage of the knowledge that P = 1. If P = 1 AND Y = 0, then Q = 1. It doesn't matter what P is, as long as Y = 0, Q will be 1.
• That gives us the first entry in the truth table above. Here's the truth table with what we have figured out so far.

  X	Y	P	Q
  0	0	1	1
  0	1
  1	0
  1	1

• If X = 0, then P = 1. We know that if either input to a NAND gate is 0, the output is 1. That's the same as before.
• Now. try to take advantage of the knowledge that P = 1. If P = 1 AND Y = 1, then Q = 0.
• That gives us the second entry in the truth table above. Here's the truth table with what we have figured out so far.

  X	Y	P	Q
  0	0	1	1
  0	1	1	0
  1	0
  1	1

• If X = 0, then P = 1. We know that if either input to a NAND gate is 0, the output is 1. That's the same as before.
• Now. try to take advantage of the knowledge that P = 1. If P = 1 AND Y = 1, then Q = 0.
• That gives us the second entry in the truth table above. Here's the truth table with what we have figured out so far.

  X	Y	P	Q
  0	0	1	1
  0	1	1	0
  1	0
  1	1

• If Y = 0, then Q = 1. We know that if either input to a NAND gate is 0, the output is 1. That's the same as before. However, this time, we take advantage of knowing that Y = 0. Before, it was X that was equal to zero, but X = 1 here and it doesn't help us get started.
• Now. try to take advantage of the knowledge that Q = 1. If Q = 1 AND X = 1, then P = 0.
• That gives us the third entry in the truth table above. Here's the truth table with what we have figured out so far.

  X	Y	P	Q
  0	0	1	1
  0	1	1	0
  1	0	0	1
  1	1

• If X = 1, then we need to know Q to determine P.
• If Y = 1, then we need to know P to determine Q.
• We are stuck! There is no obvious way to proceed!

• If Y = 1, and P = 1, then we know that Q = 0.
• If we know that Q = 0, it is an input to the top NAND gate, so the output there is 1. Thus, P = 1. That's what we assumed to start with, so we don't get a contradiction.
• All is copasetic! Or is it?
• Here is the truth table.

  X	Y	P	Q
  0	0	1	1
  0	1	1	0
  1	0	0	1
  1	1	1	0

• This result is not at all intuitive.
  • The circuit is symmetric.
  • If we have symmetric inputs (X = 1, Y = 1), we should have symmetric outputs.
  • Instead, we seem to have shown that P = 1 and Q = 0. That's not at all symmetric, and it it bothersome.
• We got to the result by making an unsymmetrical assumption. We assumed P = 1.

• If P = 0, then Q = 1 since P is an input to the bottom NAND gate.
• If we know that Q = 1, it is an input to the top NAND gate, so the output there is P = 0 since the other input to the top gate, X, is also 1.
• But, P = 0 is what we assumed to start all this. Again, we do not get a contradiction, so everything seems OK.
• Here is the truth table for this situation.

  X	Y	P	Q
  0	0	1	1
  0	1	1	0
  1	0	0	1
  1	1	0	1

There's something decidedly peculiar here. The output has to be one or the other of these two cases. Which is it?

But, there's a related question.

• When you were little and went to the playground, when you walked up to the see-saw, which direction did the see-saw tilt? Or did you call it a teeter-totter?
• Like the see-saw/teeter-totter, this circuit depends upon what went on before.
• It can exist in either state. The see-saw can tilt in either direction. Which state you find depends upon history.
• This circuit has a name with that same-consonant-different-vowel property. It's called a flip-flop.

• Let us assume that we input X = 1 and Y = 0. Then, the output will be P = 0, Q = 1. Here is the flip-flop in that state

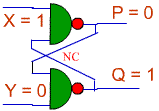
• Then, consider what happens when Y changes from 0 to 1. Since P = 0, Q will not change when Y changes. It only takes one zero input to keep the output of a NAND gate at one. That means that the output does not change when Y changes to 1.

• Let us assume that we input X = 0 and Y = 1. Then, the output will be P = 1, Q = 0. Here is the flip-flop in that state

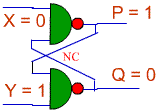
• Now, consider what happens when X changes from 1 to 0. Since Q = 0, P will not change when X changes. It only takes one zero input to keep the output of a NAND gate at one. That means that the output does not change when X changes to 1.

• This circuit is a prototype of a memory element. It can store and remember one bit of information.
• Before it's a good memory element, it will need a little work.
• The method we used to determine possible states in the flip-flop, including especially the case of inputs with two possible stable states, is the method of contradiction.