Logic Functions
Logic Functions
In the first lesson on
digital logic we examined how you could use truth tables and gates to produce an
electrical implementation of a given truth table. In this lesson you will
examine that process more formally.
Larger logic problems
require a systematic approach for solution. Modern integrated circuit chips -
for example CPU chips for personal computers - can use millions of logic
devices. The sheer magnitude of these designs is a clear sign that a formal
approach to the design is needed.
In this lesson you will
learn some ways of using Boolean algebra expressions that point directly to a
particular logic circuit implementation. We will finish the lesson by examining
a way to simplify circuits so that they use a minimum number of components and
gates.
Here are your goals
for this lesson - what you should be able to do.
Given a Boolean function described by a truth table,
Be able to determine the smallest sum of
products function that has the same truth
table.
Be able to determine the AND-OR-NOT
circuit that implements that smallest sum of products function.
Be able to determine the all-NAND
circuit that implements that smallest sum
of products function.
Minterm Expansions
There are usually numerous
ways any Boolean function can be expressed, and each expression leads fairly
naturally to a circuit with AND gates, OR gates and inverters. Different ways
of expressing a function can have widely varying levels of complexity. More
complex circuits will require more gates and inverters, so it's a reasonable
goal to learn how to devise circuits that are as simple as possible.
In this section we are
going to look at how you can represent circuits differently using Boolean
algebra. We'll move from that to a consideration of how you can implement
circuits based on different Boolean expressions. Those concepts are important
because any given circuit, even one as complex as a CPU chip, will be better if
you can design it to use fewer components. That's expecially important in large
circuits involving millions of transistors or gates. Savings of a small
percentage of components can translate into thousands of transistors or gates.
An Example Function
Let's look at a simple
Boolean function of three variables. We'll describe this function with a truth
table. Here's the truth table. The input variables are X, Y and Z, and the
function output is F.
| X
|
Y
|
Z
|
F
|
| 0
|
0
|
0
|
0
|
| 0
|
0
|
1
|
0
|
| 0
|
1
|
0
|
1
|
| 0
|
1
|
1
|
0
|
| 1
|
0
|
0
|
0
|
| 1
|
0
|
1
|
1
|
| 1
|
1
|
0
|
0
|
| 1
|
1
|
1
|
0
|
Let's examine this
function in some detail. The only non-zero entries are at:
X = 0, Y = 1, Z = 0
and
X = 1, Y = 0, Z = 1
The function is
1 for those two input
conditions and zero for all other input conditions.
Now, lets' think about how
we can implement this function. Here's a description of what we want to
implement:
- We want the output to
be 1 whenever we
have either
- OR
when we have
This word statement is very
close to the function we want. We've highlighted the important aspects of the
function. Here's the function:
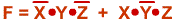
This function is
read as (NOT-X AND Y AND NOT-Z) OR (X AND NOT-Y AND
Z) and when we read
NOT-X that means we have to have
X=0 to make the three terms
ANDed together work
out to 1.
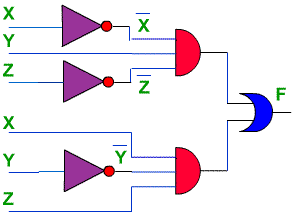
Now, let's look at a
circuit that will implement this function. Here's the circuit. Notice how the
inputs are grouped into groups of 3, ANDed together (after taking inverses where
appropriate) and the results ORed at the end.
Defining Minterms
In producing our circuit
we had to use the form:
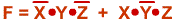
. This form is composed of
two groups of three. Each group of three is a minterm. What the expression
minterm is intended to
imply it that each of the groups of three in the expression takes on a value of
1 only for one of the
eight possible combinations of X, Y and Z and their inverses. Important points
about minterms include the following.
- In a minterm, each variable,
X, Y or Z appears once, either as the variable itself or as the inverse.
- Each minterm corresponds to
exactly one entry (row!) in the truth table.
Implications of the two
points above are that you can build any Boolean function at all by building it
up from minterms. There is no qualification to this statement. Truly any
Boolean function can be constructed using minterms, and the construction process
is simple.
To build any Boolean
function from minterms do the following.
- Get a truth table for the
function. Be sure that all possible combinations of variables and inverses
are accounted for.
- For each entry of the
truth table for which the function takes on a value of
1, determine the
corresponding minterm expression remembering that every variable of its
inverse will appear in every minterm.
- OR
all the minterms from the second step together.
We can sum up this conclusion
with the following:
- A truth table gives a unique
sum-of-products function that follows directly from expanding the ones in
the truth table as minterms.
An Example Using Minterms
To illustrate the
use of minterms to get an electrical implementation of a logic circuit, consider
this problem. Three young graduates have formed a company. The three
graduates, Alisha, Ben and Corey have a system to minimize friction. For all
minor decisions they want to use a circuit that will determine when a majority
of the three of them has voted for a proposal. Essentially, they want a box
with three inputs that will produce a 1
at the output whenever two or more of the inputs are
1.
The solution process
starts by getting the truth table. That's shown below. Notice that there are
four 1 entries in the
table. Those 1s occur
when two people vote Yes
together or when all three vote together.
| A
|
B
|
C
|
V
|
| 0
|
0
|
0
|
0
|
| 0
|
0
|
1
|
0
|
| 0
|
1
|
0
|
0
|
| 0
|
1
|
1
|
1
|
| 1
|
0
|
0
|
0
|
| 1
|
0
|
1
|
1
|
| 1
|
1
|
0
|
1
|
| 1
|
1
|
1
|
1
|
After getting the
truth table, the next step is to identify the minterms. That's shown below
where the minterms are to the right of the corresponding entries in the truth
table. There are four 1
entries in the truth table and four corresponding minterm expressions.
| A
|
B
|
C
|
V
|
| 0
|
0
|
0
|
0
|
| 0
|
0
|
1
|
0
|
| 0
|
1
|
0
|
0
|
| 0
|
1
|
1
|
|
| 1
|
0
|
0
|
0
|
| 1
|
0
|
1
|
|
| 1
|
1
|
0
|
|
| 1
|
1
|
1
|
|
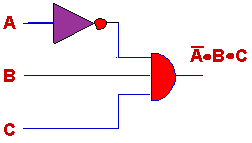
The first term, where Ben
and Corey vote YES, and Alisha votes NO is this term. Note that this term
corresponds to:
- A = 0 - which means NOT-A
is 1
- B = 1
- C = 1
so, when you AND all these
terms together, you get 1
under the conditions here.
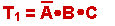
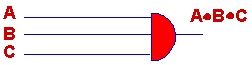
There are three other terms and we
could make similar observations about them.
   
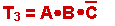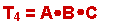
Now, with the minterm
expressions, we can write an expression for the 3-person voting function, V. We
have:
This expression leads directly to
a circuit implementation using ANDs, ORs and Inverters. Each minterm can be
generated using a 3-input AND gate. The first minterm is shown below.
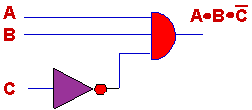
You'll need three more
circuits somewhat like this one for the complete solution. Now, you should be
able to construct the other three. They are similar to the one above. Here
they are. Each circuit shows the output term from the truth table.
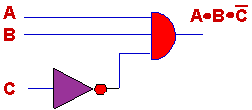
Next, consider how these small circuits
must interact. The function is 1 whenever the
first term is 1, OR when the second term is
1, OR when the third term is
1, OR when the fourth term is 1. To
implement that you need the following circuit.
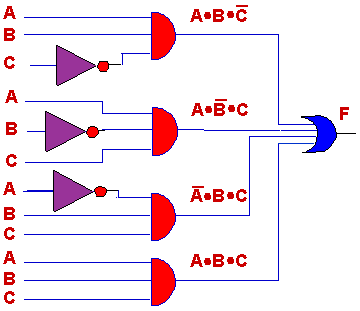
Keep in mind how this circuit comes about. Each
AND gate senses just one of the terms in the truth table, and is
1 whenever that corresponding element in the table
is selected (by selecting the correct inputs for that point in the truth table.
In the expression we saw earlier, the outputs of each AND gate are ORed together
to produce the output. Here's that function again.
Be sure that you can see how the circuit above
implements this function.
This function is composed of four
minterms, and as noted above each minterm
corresponds to one entry of 1 in the truth table. That implies the following
algorithm for generating a Boolean algebra function from a truth table.
- Given a truth table
with one or more places in which the function takes on a value of
1,
- Write out the
minterms for each place in the table where the function takes on a value
of 1.
- OR
all of those minterms together.
Note the properties of this algorithm:
- It will always work to allow
you to generate a Boolean function from a truth table.
- The Boolean function
will be a number of minterms ORed
together
- The number of
minterms will be the number of places (1s)
in the truth table where the function takes on a value of
1.
- This kind of
function is often referred to as a "sum of
products" form.
- The sum of products
form leads directly to a "two layer"
implementation with ANDs
in the first layer and a single OR
in the second layer.
- The number of
ANDs will be
the number of places (1s)
in the truth table where the function takes on a value of
1.
- That's one AND gate for
every minterm in the sum of products form you get for the function.
- When we say two layers,
we are ignoring the possibility that you might require some inverters
(NOTs) to complement some of the input signals. (On the other hand,
those inverted signals might be available in the system, and you might
not need the inverters!)
Using minterms is not always
the most efficient way to implement a circuit. Although a minterm expansion
will always produce a function you can implement, for any truth table, there are
better ways - ways that use fewer gates and which therefore cost less to
implement. We'll look at those next.
|
