D/A Converters
Why Interface Circuits?
Computers don't exist in a vacuum. They have to interface with the world
in many ways. You can sit at a keyboard and type and you're using a
computer interface. You click a mouse button and that's another interface.
Measurement devices often need to communicate with computers also.
There are
numerous other situations where you need to have a computer produce a specific
voltage for some purpose.
Goals
Here's
what you should be able to do after this lesson.
A Simple Digital To Analog
Converter
We are
going to start by examining a simple circuit. This circuit is an
operational amplifier circuit with three input voltages.
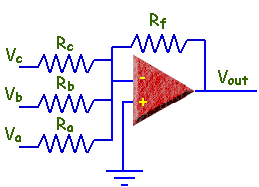
-
Each input voltage is either
zero volts or five volts and represents a logical 0 or 1.
-
The input resistors are chosen
so that they are not all equal.
-
The resistors are related by:
Rc = 2Rb = 4Ra.
To
understand how this circuit works we will need to obtain a symbolic expression
for the output voltage - one in which we express the output voltage in terms of
the binary number that the input represents. We already have an expression
for the output voltage.
Vout
= (RfVa /Ra) + (RfVb
/Rb) + (RfVc /Rc)
We need to interpret this output voltage
expression when the inputs represent a binary number.
Let's examine the expression for the output voltage using the relation we
required for the resistors.
Rc
= 2Rb = 4Ra
Then, the output voltage expression becomes:
Vout
= (RfVa /Ra) + (RfVb
/Rb) + (RfVc /Rc)
Vout
= (RfVa /Ra) + (RfVb
/2Ra) + (RfVc /4Ra)
Each
input voltage is either zero (0) or five (5) volts, representing either a zero
or a one. Although we shouldn't mix Boolean algebra variables and ordinary
algebraic variables, we are going to. We're going to say
Va
= 5A2
Vb
= 5A1
Vc
= 5Ao
So
Vout
= (Rf/4Ra)(4Va + 2Vb
+ Vc )
Vout
= (5Rf/4Ra)(4A2 + 2A1
+ Ao )
And, the question we are left with is "What is (4A2
+ 2A1 + Ao
)?"
The expression - (4A2 + 2A1 + Ao
) - can be regarded as the binary number represented by A2, A1
and Ao. This table shows the equivalence.
|
A2
|
A1
|
Ao
|
Binary #
|
4A2+2A1+Ao
|
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
1
|
1
|
|
0
|
1
|
0
|
2
|
2
|
|
0
|
1
|
1
|
3
|
3
|
|
1
|
0
|
0
|
4
|
4
|
|
1
|
0
|
1
|
5
|
5
|
|
1
|
1
|
0
|
6
|
6
|
|
1
|
1
|
1
|
7
|
7
|
In other words, A2
is the 4 bit, A1 is the 2 bit and Ao
is the 1 bit.
After all this, we reach these conclusions for this circuit.
-
The inputs can be thought of as
a binary number, one that can run from zero (0) to seven (7).
-
The output is a voltage that is
proportional to the binary number input.
-
The circuit itself converts a
digital representation of a number to an analog version of the same number.
The circuit is a digital-to-analog converter also known as a D/A converter.
What if we wanted to convert a digital signal with more bits? The answer
to this question should be fairly obvious.
-
More input resistances are
needed.
-
The resistances should be
chosen in ratios of 2.
-
The LSB has the largest
resistance.
-
More significant bits have
resistances that decrease by a factor of 2.
Next, we're going to look at some circuits that use the D/A converter.
-
One application of a D/A
converter is to convert signals generated within a computer to voltages outside
the computer. Examples where this is useful include control systems, where
a control signal could be calculated by a computer (implementing some known
control algorithm) and then converted to a voltage using a D/A converter.
That voltage could end up driving a motor for a pump - among many other things
that might occur.
-
D/A converters also occur
within larger systems.
-
A pulse generator generates a
pulse train - a sequence of zeros and ones.
-
The pulse train is counted by a
counter.
-
The counter output is the input
to the D/A.
-
The D/A output is compared to
the voltage input, and when the D/A output exceeds the voltage input, the
comparator output changes state and stops the counter.
The second example is really an A/D converter. It's interesting that many
A/D converters contain D/A converters within them. D/A converters are
often emedded in places where you might not expect to find them. You use
them all the time.
You may not think that you have ever used a D/A, but we will convince you that
you have. We'll do that by having you use one you have used before.
First, we need a source of digital signals that we can convert to analog
signals. The most common source like that is a music CD. Consider
what happens when you play a music CD. (Note, we're deliberately
emphasizing the phrase music CD because we want to emphasize it is not a CD with
program files on it that we want to use.)
-
Your CD has tiny little pits on
the surface. You can't really see them, but they are there.
-
A low power laser is flashed on
the CD, and the reflectivity is different where there is a pit. That means
that the reflected laser signal can be used to read the zeroes and ones on the
CD.
-
So, as the CD spins in the
holder, a sequences of zeroes and ones is generated and sent on.
-
That sequence of zeroes and
ones is converted to an analog voltage that is amplified and fed to an earphone
or a speaker.
-
So, you see that you have used
an A/D before - if you have ever used a CD player.
|

