Phasors

• = V_sum,real + jV_{sum,imaginary}

• And, the phasor for the sum voltage can also be represented with a magnitude-angle representation.

• = V_sumcos(f_sum) + jV_sumsin(f_sum)

        There is, of course, also a geometrical interpretation whenever you deal with complex numbers or variables.  If we have two phasors that we are adding, we visualize the situation as shown below.

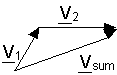
V_sum = V₁ + V₂

        We can add the two phasors any way possible.  That includes doing it graphically by hand, breaking the phasors into components and summing the real and imaginary components - as we did above - or any other way you can imagine to sum two vector-like quantities.

Differentiation of Time Functions Represented by Phasors

       A second operation that we need to perform often is differentiation of a time function represented by a phasor.  Consider a sinusoidal time function, v(t):

with a phasor V:

The derivative of the time function is given by:

The phasor for the derivative signal is:

(Note the minus sign on the first represention where ninety degrees is subtracted has been eliminated when the angle is changed to plus ninety degrees!)

We conclude the following.

• Differentiating a sinusoidal signal is equivalent to multiplication of the signal's phasor by w and rotation of the phasor by 90^o.

        There is also an interpretation in terms of complex numbers.  Represent the phasor V in terms of complex numbers:

Then, consider the phasor for the derivative:

But, we can also write the phasor for the derivative from the time function for the derivative.

Now, work with this expression.

• Take the ninety degree terms out of the arguments since:

• cos(f+90^o) = -sin(f), and sin(f+90^o) = cos(f).

and with some insight, we can note that this is the same as (since j² = -1):

The conclusion:

• Differentiating a sinusoidal signal is equivalent to multiplication of the signal's phasor by jw.

        There is a little side note here that is important.  When you study Laplace transforms you will find that differentiating a signal - any signal, not just a sinusoid - is equivalent to multiplication of the signal's Laplace transform by the Laplace transform variable, s.  The similarity is not an accident.  The Laplace transform is a generalization of the Fourier transform, and the Fourier transform is based on the idea that a signal - almost any signal - can be represented as a sum of sinusoids.  In the case of the Fourier transform, that sum becomes an integral.  When you travel this road, you go through Fourier Series, then get to Fourier transforms and finally you get to Laplace transforms.  Not everybody takes all of the steps, and some might jump directly to Laplace transforms, but viewing the entire path can be enlightening.

Example

E1

        In a capacitor, the voltage and current are related by:

so the voltage phasor, V_c, and the current phasor, I_c, are related by:

E2   Imagine that you have two voltage sources in series as shown below.

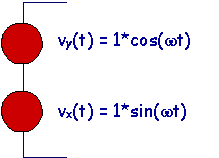
These two voltages are both sinusoidal, but at different phases.  You can see the voltages in this simulator.

• To see the cosine term, type a "1" in the cosine term text-box and be sure that the cosine term stays zero.

• To see the sine term, type a "1" in the sine term text-box, and set the cosine term to 0.

       We leave this as an exercise for the interested student.

• The time integral of a sinusoidal signal is equivalent to multiplication of the signal's phasor by 1/jw.

A Quick Summary of What You Need to Know

        Phasors are used extensively in AC circuit analysis.  Operations you need to be familiar with include addition and differentiation in the time domain, and the corresponding results for the phasors representing the time domain signals.