| Error Propagation |
Error Propagation
Given a
formula
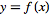 with an
absolute error in
with an
absolute error in
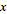 of
of
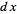 ,
the
absolute error is ,
the
absolute error is
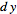 .
The
relative error is .
The
relative error is
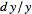 .
If .
If
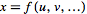 ,
then ,
then
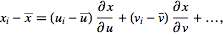 |
(1)
|
where
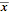 denotes the
mean, so the
sample variance is given by
denotes the
mean, so the
sample variance is given by
The definitions of
variance
and
covariance then give
(where
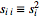 ),
so ),
so
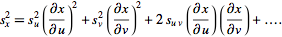 |
(7)
|
If
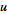 and
and
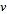 are uncorrelated, then
are uncorrelated, then
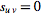 so
so
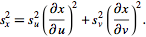 |
(8)
|
Now consider addition of quantities with errors. For
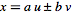 , ,
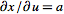 and
and
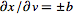 ,
so ,
so
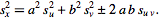 |
(9)
|
For division of quantities with
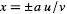 , ,
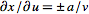 and
and
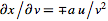 ,
so ,
so
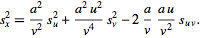 |
(10)
|
Dividing through by
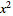 and rearranging then gives
and rearranging then gives
For exponentiation of quantities with
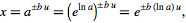 |
(14)
|
and
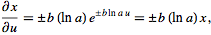 |
(15)
|
so
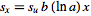 |
(16)
|
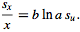 |
(17)
|
If
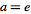 ,
then ,
then
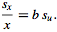 |
(18)
|
For
logarithms of quantities with
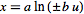 , ,
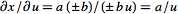 ,
so ,
so
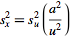 |
(19)
|
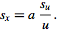 |
(20)
|
For multiplication with
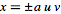 , ,
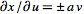 and
and
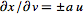 ,
so ,
so
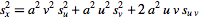 |
(21)
|
For
powers,
with
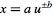 , ,
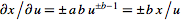 ,
so ,
so
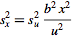 |
(24)
|
|