| Thevenin's Theorem |
Thevenin's Theorem
In the first few parts of this series, we've used "differential Ohm's Law,"
Kirchoff's Current Law, Kirchoff's Voltage Law, node voltage analysis, and mesh
analysis to analyze a simple three resistor circuit (figure 1). This time, we'll
use Thevenin's Theorem to simplify the circuit, which cannot be analyzed
by Ohm's Law by itself, down to something that can be analyzed
using Ohm's Law. We'll also look at a couple ways to analyze a Wheatstone Bridge
circuit using Thevenin's Theorem.
In doing research for this article, I found hundreds of books that discussed
the application of Thevenin's Theorem, but very little about its origin. I
did find that Thevenin's Theorem was apparently first published by Herman
Von Helmholtz (1821 - 1834) in 1853. Helmhotz was a German scientist who worked
in a wide variety of sciences. He was originally trained as a doctor, since the
German government would pay for his training if we would then serve in the
military. One reference stated "Helmholtz was the last scholar whose work, in
the tradition of Leibniz, embraced all the sciences, as well as philosophy and
the fine arts." I was unable to find a translation of his original stating of
this theorem.
M. L. Thevenin (1857 - 1926), a French telegraph engineer, again discovered
the theorem in 1883 (see rendus hebdomadaires de seances de L'Academie des
sciences, XCVII, 159 (1883), excuse my French!).
Finally, I also found a reference to it as the Thevenin-Pollard theorem. And,
in 1926, E. L. Norton of Bell Telephone Laboratories replaced the voltage
sources in the Thevenin (or whoever) equivalent with current sources to come up
with the Norton equivalent. We'll look at Thevenin equivalents this time and
Norton equivalents in a later article.
Thevenin Equivalent
A circuit containing linear devices (whose current is proportional to the
applied voltage) and independent sources can be replaced with a single voltage
source with a single series impedance for analysis. This Thevenin equivalent
can replace the original complicated subcircuit in the original circuit. The
use of the equivalent circuit should simplify (or make possible) the analysis of
the original circuit. It should be noted that the equivalent circuit is
only equivalent outside the equivalent. You cannot make
efficiency calculations of the original subcircuit based on its equivalent.
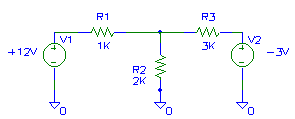
Figure 1 - Circuit to be analyzed.
Let's find the Thevenin equivalent of the "left half" of the circuit
(replacing V1, R1 and R2). Other equivalents are possible, but care must be
taken that you don't replace too much of the circuit with the equivalent,
leaving points of interest "inside" the equivalent where they are not available
for analysis. Figure 2 shows the circuit we wish to "Thevenize". Figure 3 shows
how it has been replaced by a single "Thevenin voltage" and a single "Thevenin
resistance".
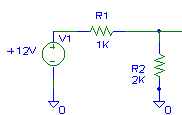
Figure 2 - Circuit to be Thevenized.
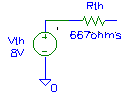
Figure 3 - Thevenin equivalent of figure 2
To determine the Thevenin voltage take the original circuit for which
the equivalent is desired (figure 2), and place an "imaginary voltmeter" across
the two terminals that connected this subcircuit to the remainder of the
circuit. In this case, we measure the voltage at the junction of R1 and R2 with
respect to ground. This "open circuit voltage" is the Thevenin voltage. In this
circuit, it was easily determined using Ohm's Law or using the voltage divider
formula (12V*(2K/3K)=8V).
To determine the Thevenin resistance (or, in AC circuits, the
Thevenin impedance ), replace all independent voltage sources with zero volt
sources (a short) and replace all independent current sources with zero amp
sources (an open). Place an "imaginary ohmmeter" the same place we put the
voltmeter above. In this case, the shorting of V1 puts R1 in parallel with R2,
yielding a Thevenin resistance of 667 ohms. The Thevenin equivalent of
figure 2 is shown in figure 3. Figure 4 shows the original circuit with V1, R1
and R2 replaced by their Thevenin equivalent.
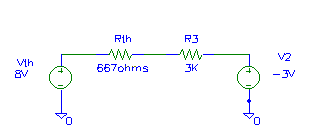
Figure 4 - Original circuit with equivalent.
Differential Ohm's Law, Again!
We can apply "differential Ohm's Law" to the circuit of figure 4 to determine
circuit characteristics. First, we establish the direction of conventional
current, which "flows downhill," from high (more positive) voltage to low
(less positive or more negative). Here, the conventional current flows to the
right. We can then determine that current using I=(Vtail-Vtip)/R. Vtail is +8
volts, while Vtip is -3 volts. R is the series combination of Rth and R2:
3.667K. The current is 3mA.
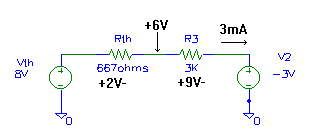
Figure 5 - Analyzing the equivalent circuit.
Using Ohm's Law, we can determine the voltages across Rth and R2, as shown in
figure 5. To determine the voltage at the junction of Rth and R3, we can start
at the right side of R3, which is at -3 volts due to V2, then "go up" 9 volts as
we pass through R3 to the left. This puts the junction at +6 volts, as shown. We
could also start at the top of Vth (+8 volts) and go down 2 volts as we go to
the right through Rth. Again, we get +6 volts.
Back to the original circuit!
Once we know the voltage at the left end of R3, we can drop this information
into figure 1 and determine any other desired currents. Note that this
determination agrees with our previous calculations using node voltage analysis,
mesh analysis, and superposition.
Next time, we'll try applying two Thevenin equivalents to the
Wheatstone bridge. Your homework assignment is to find out who Wheatstone was,
and why he got a bridge named after him.
|

