Using Thevenin Equivalents on Wheatstone Bridge
SAN LUIS OBISPO, Calif. Last month, we used Thevenin
equivalents to analyze a simple resistive T network. One of the more common
applications of Thevenin equivalents is in the analysis of an unbalanced
Wheatstone Bridge.
The Wheatstone bridge is named after Sir Charles Wheatstone
(1802-1875), an English physicist and inventor. The Wheatstone bridge was first
described by Samuel Hunter Christie (1784-1865) in his paper Experimental
Determination of the Laws of Magneto-electric Induction (1833). The circuit
was brought into general use by Wheatstone in 1843. Samuel Christie was the son
of James Christie, founder of the well-known auction galleries (see
Dictionary of Scientific Biography; Charles Coulston Gillispie, editor). The
bridge was (and is) used chiefly to measure resistance. Substituting resistances
and reactances for the reference resistance in the bridge, and driving the
bridge with AC, allows it to be used to measure impedance.
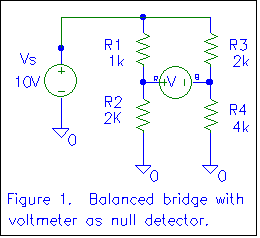
Figure 1 shows a simple balanced Wheatstone bridge with a voltmeter as a
null detector. Let's determine the voltage indicated by the voltmeter.
The voltage on the left side of the voltmeter (marked R for the red or
positive lead) with respect to ground can be determined using the voltage
divider formula as
VR = (R2/(R1+R2))*10V = (2K/3K)*10V = +6.667 volts
The voltage on the right side of the voltmeter (marked B for the black,
negative, or reference lead) with respect to ground can also be
determined using the voltage divider formula as
VB = (R4/(R3+R4))*10V = (4K/6K)*10V = +6.667 volts
VRB is the voltage a point R with respect to point B. Further, VRB
= VR - VB. So, in this case, VRB = 0 volts. We
say the bridge is balanced.
We can see that the bridge is balanced if VR = VB. We
can generalize this as
VR = VB
(R2/(R1+R2))*VS = (R4/(R3+R4))*VS
R2/(R1+R2) = R4/(R3+R4)
R2*(R3+R4) = R4*(R1+R2)
R2*R3 + R2*R4 = R4*R1 + R4*R2
R2*R3 = R4*R1
R2/R1 = R4/R3
We now see that the ratio of the resistances in each "arm" of the bridge
determines whether the bridge is balanced. Further, if the bridge is balanced,
we can substitute an ammeter (ideally zero resistance) for the voltmeter and
read zero current. If we have the same voltage at two points in a circuit and
connect them together (through the ammeter), no current will flow.
An Unbalanced Bridge
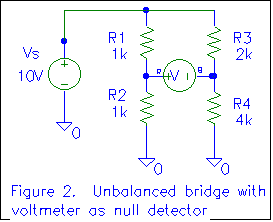
Consider the circuit of figure 2. We can see right away that the bridge is
not balanced, based on the resistance ratios (as derived above). What will
the voltmeter read?
VR = (1K/(1K+1K))*10V = +5 volts
VB = (4K/(2K+4K))*10V = +6.667 volts
VRB = +5 volts - 6.667 volts = -1.667 volts
Note that the voltage is negative. If we were to reverse the voltmeter
leads, the voltage would be positive. However, as long as we specify the voltage
as VRB, the voltage is negative, and polarity is important.
The Loaded Unbalanced Bridge
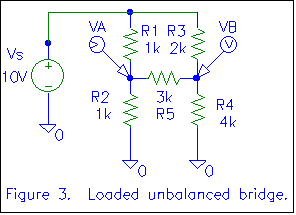
Figure 3 shows a loaded unbalanced bridge. We can still use the resistance
ratios derived above to determine that the bridge is indeed unbalanced (current
will flow through R5), but we cannot determine how much current flows
through R5 without using a technique beyond simple voltage dividers. The
"voltage divider formula" works only in a simple series circuit, where
all the current flowing in one resistor flows in all the resistors. In figure 3,
the current through R1 will equal the current through R2 only if there is
no current through R5 (Kirchoff's current law), and we have determined there is
current through R5, since the bridge is unbalanced. We'll use Thevenin
equivalents to determine the current through R5, along with all the other
circuit parameters (We'll "analyze it to death").
Although it is quite possible (and appears standard) to bring the bridge down
to a single Thevenin equivalent, I prefer to make two equivalent circuits, one
for the left half of the bridge and one for the right half. This approach allows
us to determine all the circuit node voltages from the equivalent circuit while
the typical "single equivalent" approach only yields the "load current" (the
current through R5).
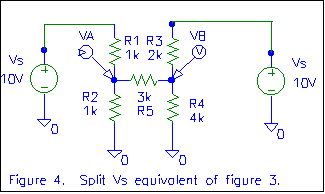
In figure 4, we've split VS into two equivalent sources. At this
point, we could determine the circuit parameters (VA and VB
would be most useful) using superposition. Give it a try! Apply the voltage
sources one at a time, substituting a short for the voltage source that is out
of circuit. Determine VA and VB when each of the sources
is present (VA due to the left source and due to the
right source), then add the results to yield the total VA and total VB.
It should match what we come up with.
Figure 5 shows a the circuit of figure 4 with Thevenin equivalents for each
"half" of the circuit. V12 is the Thevenin voltage formed by the left 10 volt
source, R2, and R1. It is the voltage measured at the junction of R1 and R2
(point A) with R5 disconnected. Since this then becomes a simple voltage
divider, V12 is (R2/(R1+R2))*10V, or 5 volts.
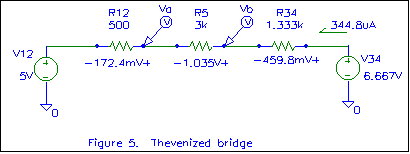
R12 is the Thevenin resistance of the left half of the circuit. This is
determined by shorting out all voltage sources and measuring the resistance
between point A and ground, with R5 removed. The shorted voltage source results
in R1 being in parallel with R2, so the Thevenin resistance is 1K//1K or 500
ohms.
Similarly, V34 is the Thevenin voltage formed by the right 10 volt source,
R4, and R3. It is the voltage measured at the junction of R3 and R4 (point B)
with R5 disconnected. Since this also becomes a simple voltage divider, V34 is
(R4/(R3+R4))*10V, or 6.667 volts.
In figure 5, these Thevenin equivalents are substituted for the original
voltage sources and R1, R2, R3, and R4. R5 is carried to the equivalent circuit.
The unbalanced loaded bridge has become a simple series circuit that can be
analyzed using "differential Ohm's law". The current through the resistors is (Vtail-Vtip)/R,
or (6.667V-5V)/4.833K = 344.8uA. This current can then be multiplied by the
resistance of each resistor to get the voltage across that resistor. Note
the marked voltage polarities and the current direction. I think these are
very important! With conventional current, the current flows downhill
(from higher voltage to lower), so that is the way the arrow was drawn. If the
arrow had been drawn the other way, we would get a negative current. A negative
current going to the right is equivalent to a positive current going to the
left. Further, with a positive conventional current, the voltage across a
resistor will be positive on the end the current enters and negative on the end
the current leaves.
We can verify our calculations by using Kirchoff's Voltage Law (the sum of
the voltage rises or drops around any closed loop is zero). If we add the
voltage rises, starting at the bottom of the left battery, we find we have 5V +
172.4mV + 1.035V + 459.8mV - 6.667V = 200uV, which is close to zero. The
only reason it's not exactly zero volts is due to rounding errors in our
calculations. Close enough!
To determine the voltage at any point in the circuit, we can start at a point
where we know the voltage (with respect to ground) and "wind" our way through
the circuit accumulating voltage rises and drops. For example, to determine the
voltage a point A, we can start at ground on the left side of figure 5. Ground
is zero volts. We "go up" 5 volts as we go through V12, since we are "coming
out" the positive side of V12 as we work our way towards point A. We go up an
additional 172.4 mV as we go through R12, since we are also coming out the
positive side of R12. This makes VA 5.1724 volts.
We could have determined VA starting below the right voltage
source. In that case, we start at zero volts below the source, go up 6.667 volts
going through V34, go down 459.8mV as we go through R34 (since we are coming out
the negative end), then go down an additional 1.035 volts as we go through R5.
In this case, VA = 6.667V - 459.8mV - 1.035V = 5.1722 volts. The
minor difference is, again, due to rounding.
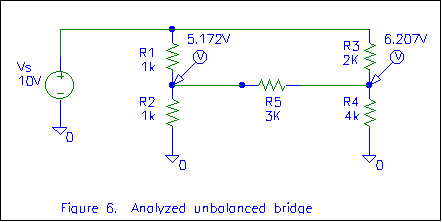
We have a couple ways of finding VB. Let's just say it's 1.035 volts
above VA or 6.207 volts. These voltages are substituted back in the
original circuit in figure 6. Once these voltages are known, all node voltages
in the circuit are known. Differential voltages can be easily determined by
subtracting (VAB=VA-VB). Current through any
component can be determined by "differential Ohm's law". By making these
calculations, we can "analyze the circuit to death". As practice, try showing
that the sum of the currents into the node at the junction of R1, R2, and
R5 is zero (Kirchoff's current law). I get 4.828mA + (-5.172mA) + 345uA = 1uA.
Pretty close!
Next time we'll look at Norton equivalents, followed by Millman's Theorem.
Ten extra points to anyone who sends me biographical information on Norton or
Millman.
|

