| Analyzing Circuits with Norton |
Norton Equivalents
SAN LUIS OBISPO, Calif. Last month, we used Thevenin equivalents to
analyze a Wheatstone Bridge circuit (which, as you may recall, was first
described by Samuel Hunter Christie in 1833). Let's convert the voltage sources
in the Thevenin equivalent to current sources and move the Thevenin resistance
from in series with the voltage source to across the current source. This is the
Norton Equivalent, a technique described by E. L. Norton of Bell Telephone
Laboratories in 1926. Next month we'll generalize this a little and get
Millman's Theorem.
I recently received a fax from George Pfisterer, Jr of Huntingdon Valley, PA.
Mr. Pfisterer recalls working in the Data Communications Department of Bell
Telephone Laboratories in Murray Hill, NJ. A few doors down the hall in the
building known as "Bitsburgh" was the office of Ed Norton, the originator of the
theorem we all studied. Mr. Pfisterer recalls walking past the office and
"seeing this elderly white-haired gentleman operating a giant 24 inch slide
rule." I guess a large slide rule gives a digit or two more resolution? Anyway,
Mr. Norton first described one of the fundamental theorems of circuit analysis
and 40 years later was section head in data communications. The progress in
electronics in one person's lifetime is truly phenomenal. I'm truly impressed by
the bit of the history of our field I've lived through. How about you?
Let's go back to the simple three resistor circuit we've analyzed many
times in this series. I hope that using a variety of techniques to analyze the
same circuit we'll get the same answer each time (it would be nice!), and we'll
develop a toolbox of analysis techniques.
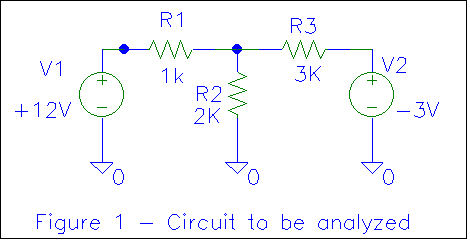
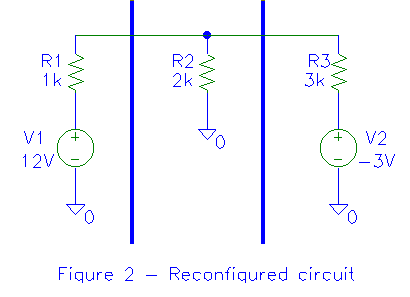
Figure 1 shows the circuit to be analyzed. In figure 2, the circuit is broken
into three parts. In figure 3, the left and right portions of the circuit are
replaced with their Norton equivalents (while the center resistor remains
unchanged).
Determining the Equivalent Circuit
Recall that in the Thevenin equivalent a complex circuit is replaced with a
single voltage source and a series resistance. Further, the Thevenin voltage was
the open circuit voltage of the original circuit. We determined this by
placing an "imaginary voltmeter" across the two terminal we were modeling and
measuring the voltage. Finally, we determined the Thevenin resistance by
replacing the imaginary voltmeter with an imaginary ohmmeter, replacing all
voltage sources with shorts, and replacing all current sources with opens. The
imaginary ohmmeter then read the Thevenin resistance.
Similarly, in the Norton equivalent, a complex circuit is replaced by a
single current source (a source that maintains a specified current
independent of the load resistance) and a parallel Norton resistance.
The Norton current is the short circuit current of the original circuit.
Whereas we placed an imaginary voltmeter across the two terminals to find the
Thevenin voltage, we place an immaginary ammeter across the two terminals for
the Norton current. We determine the Norton resistance the same way we found the
Thevenin resistance (which, incidentally, makes them the same!).
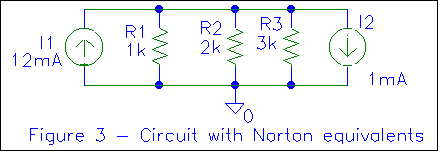
If we place an ammeter between the top of R1 and ground in figure 2
(disconnecting the top of R1 from the remainder of the circuit), we'll get the
Norton current for the left side of the circuit. Using Ohm's law, we easily see
that this is 12mA (12V/1K). The right side gives us a Norton current of 1 mA
(3V/3K). Further, note that on the left side, conventional current would flow
out of R1 (up), while on the right side, current flows into R3 (down)
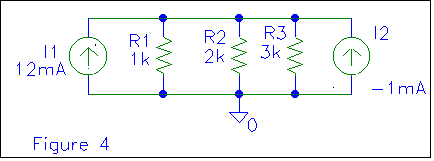
due to the polarities of the voltage sources. This difference of polarity can be
represented either as shown in figure 3 (all current sources positive) or figure
4 (all current sources pointing the same direction). For now, let's stick
with figure 4.
Current Sources in Parallel
Current sources in parallel act exactly the same as voltage sources in
series. Similarly, just as it is meaningless to put two voltage sources with
different voltages in parallel (you'll get an infinite current around the loop
as each source insists on setting the voltage), you cannot place
different current sources in series (you'll get infinite voltage out of each as
it tries to force the other to have the specified current). Just as voltage
sources in series add algebraically, current sources in parallel add
algebraically. Putting this all together, we get the circuit of figure 5, where
the two current sources (12mA and -1mA) have added to yield 11mA.
The problem of several voltage sources driving a single point through series
resistors is a common one. Millman's theorem (which we'll discuss next month)
generalizes the approach we just took to cover any number of voltage sources and
series resistances. As we look at such a general solution what do we do
with a resistor that doesn't have a voltage source in series with it
(such as R2 in this circuit)? We say it has a zero volt source in series with
it! This a very useful concept! A short (or a piece of wire) can be considered a
zero volt voltage source. No matter how much current goes throught the short,
the voltage remains zero (ideally). This is exactly the same as an ideal 12 volt
battery. No matter how much current goes through the battery, the voltage
remains 12 volts. But, a 12 volt battery seems useful, while a zero volt one
does not. The Spice circuit analysis program (available on our web pages and our
BBS) does not have an ammeter element. If you want to measure current through
some particular point in a circuit, you insert a zero volt voltage source. The
current through that voltage source is calculated by Spice.
Coming Up
Next month we'll finish up DC circuit analysis with Millman's theorem, then
move into AC circuit analysis. With AC, we'll use the same techniques we've
developed so far, but use "funny numbers" to do the math. Eventually we'll move
into active circuits, amplifiers, oscillators, modulation, and ideas about
information theory (is FM the original spread spectrum system?). I look forward
to your ideas on the route we should take on our trip.
|

