Millman's Theorem

Millman's Theorem

San Luis Obispo, Calif. In the last article in this series, we applied Norton equivalents to a simple three resistor circuit. Let's try generalizing the analysis to come up with Millman's Theorem.

Millman's Theorem is named after Jacob Millman. Mr. Millman was born in Russia in 1911 received a Ph.D. from MIT in 1935. He went on to write eight textbooks on electronics between 1941 and 1987 and was a professor of electrical engineering at Columbia University.

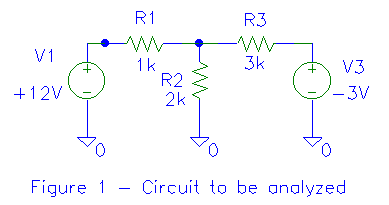
As you may recall from the last article in the series, we took the circuit of figure 1, reconfigured it as shown in figure 2, then converted the voltage sources with series resistances to current sources with parallel resistances (Norton equivalents). Note that the ground at the bottom of R₂ has been replaced with a zero volt voltage source (V₂) to ground. Recall that a "piece of wire" can be replaced with a zero volt voltage source. Adding this voltage source makes each branch of the circuit identical (a voltage source with a series resistance). Let's generalize the analysis by keeping the V's and R's, instead of substituting values.

Each voltage source with a series resistance is converted to a current source with a parallel resistance. The current is the "short circuit current" of the circuit which we are "Nortonizing". We find that I₁=V₁/R₁ , I₂=V₂/R₂, I₃=V₃/R₃. As the circuit is expanded, it's fairly obvious that I_N=V_N/R_N. Further, as we determined last time, the Norton resistance (that resistance we will place across the current source) is the same as the Thevenin resistance (that resistance in series with the voltage source). We determine the Thevenin resistance by shorting out the voltage sources and opening any current sources in the circuit we are trying to simplify, then measure the resulting resistance. 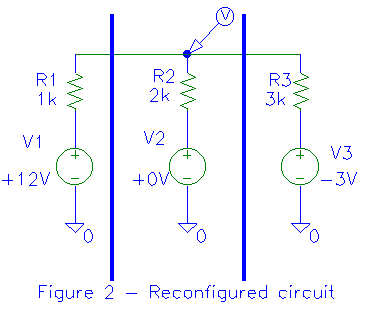For example, in the left portion of figure 2, we short out V₁, setting it to zero volts. 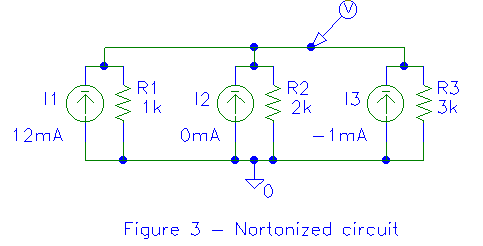We then measure the resistance from the top of R₁ to ground, getting (surprise!) R₁ ohms. Figure 3 shows the circuit of figure 2 reconfigured to use Norton equivalents for each section.

This is pretty much where we left off last time. We added the parallel current sources to get the total current and applied this to the combined parallel resistance to find the voltage at the junction of the resistances. Let's generalize it! The total current is:

Further, the equivalent parallel resistance is:

Finally, the voltage at the resistor junctions is determined by multiplying the total current by the parallel resistance (Ohm's Law):

The last equation is Millman's theorem. It might be more easily remembered by considering its components. If we replace the R in V=IR with 1/G (where G is conductance measured in Siemens) and replace V/R with I, the equation becomes:

Generalizing for any number of sources and resistances,

It would be interesting to try to derive Millman's theorem using other circuit analysis technqiues. Let's see if we can derive it using superposition next month!