| Alternating Current |
Alternating Current
San Luis Obispo, Calif. So far in this series, we've analyzed DC
circuits with a few voltage or current sources and a few resistances. Let's
start looking at alternating current. After getting a few definitions and
derivations out of the way, we'll be able to analyze circuits using the same
techniques we've used before, but use complex numbers instead of real numbers.
We'll use complex numbers to represent the magnitude and phase of voltages,
currents, and impedances.
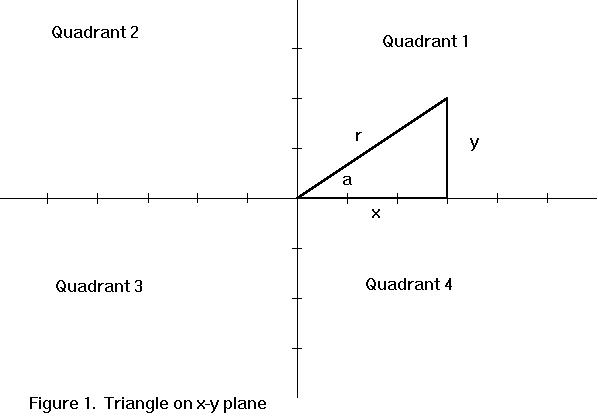
We'll start with a brief review of trigonometry. Figure 1 shows a right
triangle on the x-axis of the x-y plane. Relative to angle a, the three
sides can be identified as the adjacent, marked 'x', the opposite,
marked 'y', and the hypotenuse, marked 'r'. The adjacent side is marked
x, since it is along the x-axis. The opposite side is marked y,
since it is in the same direction as the y-axis. Finally, the hypotenuse is
marked r, since it can be thought of as the radius of a circle centered
at the origin (0,0) as the angle a is varied. Further, a point at the far end of
the hypotenuse has coordinates of (x,y) and is r units from the origin.
The three basic trig functions are shown in table 1. The first column gives
the English spelling of the function, the second gives the mathematical function
notation, and the third column shows how to calculate the function based on the
triangle shown in figure 1.
| sine |
sin(a) |
y/r |
| cosine |
cos(a) |
x/r |
| tangent |
tan(a) |
y/x |
Table 1 - Basic trig functions.
In the triangle of figure 1, we can determine r as the square root of
(x2+y2) or about 3.606. This gives makes sin(a)=2/3.606=0.555;
cos(a)=3/3.606=0.832; and tan(a)=2/3=0.667. We can use these values and the
inverse trig function to determine the angle. For example, the arctangent (tan-1)
of 0.667 is 33.7 degrees. Similarly, the arcsine (sin-1) of 0.555 and
the arccosine (cos-1) of 0.832 are both about 33.7 degrees.
If we set r = 1, then as a varies from 0 to 360 degrees, it
scribes a unit circle, a circle with a radius of 1. This simplifies the
sine and cosine as being the y and x values of the point on the
unit circle.
Above, we referred to the angle a as being measured in degrees.
A degree is 1/360 of the full cycle formed by the angle a before the
point on the unit circle returns to the point it started. We generally measure
this angle from the positive x-axis. If the point on the unit circle is in
quadrant 4 (below the positive x-axis), we can either say the angle is negative,
or say it is somewhere between 270 and 360 degrees.
We can also measure angles in radians. A radian is that angle
formed when the circle scribed by the increasing angle draws an arc length equal
to the radius of the circle. Since we know the circumference of a circle is pi
times its diameter, and the diameter is two times the radius, a the
circumference of the full circle is 2 pi r. Therefore, the full circle of 360
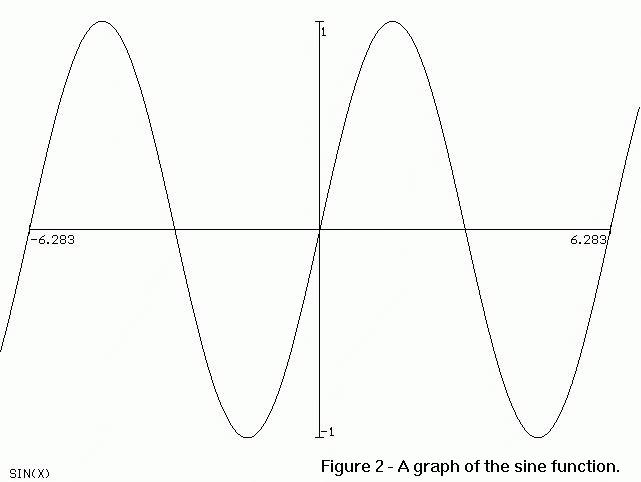
degrees is equivalent to 2 pi radians. Figure 2 shows how the sin(x) varies as x
varies from -2 pi to +2 pi radians.
Note also that the sine varies between -1 and +1. We can multiply this by a
constant and end up with a sine wave whose peak amplitude is equal to the
constant. Further, we can substitute 360*f*t for a and get a sine wave
that progresses with time, assuming the sine function expects an argument
(input) in degrees and that f is the frequency in Hz (1/seconds) and t
is time in seconds. If our sine function expects an argument in radians, we can
use wt (where w is the Greek letter omega) as the argument (the input) to
the sine function. Here, w represents the frequency in radians per
second.
In figure 3, we've set f to 1,000, and w = 2 pi f . Further,
we've multiplied the sine function by 2, giving a peak amplitude of 2. The
resulting waveform is a 2 volt peak sine wave. The amplitude (which could
represent a voltage or current) can be determined at any instant in time using
the function V(t)=2*sin(w*t) where w=2*pi*1000. This is assuming the sine
function accepts an argument in radians. If the sine function expects an
argument in degrees, the function becomes V(t)=2*sin(360*1000*t) . You might try
both of these on your calculator, then compare the results to the instantaneous
voltage indicated on an oscilloscope displaying a 2 volt peak 1 KHz sine wave.
Next time, we'll look at other characteristics of the sine wave. These
include its average value, RMS value, period and wavelength when it is
propogated. Stay tuned!
|

