Cosets and normal subgroups
3.8.2. Definition Let H be a subgroup of the group G, and let a
 G. The set G. The set
aH = { x
 G | x = ah
for some h G | x = ah
for some h  H
} H
}
is called the left coset of H in G determined by a. Similarly, the
right coset of H in G determined by a is the set
Ha = { x
 G | x = ha
for some h G | x = ha
for some h  H
}. H
}.
The number of left cosets of H in G is called the index of H in G, and is
denoted by [G:H].
3.8.1. Proposition Let H be a subgroup of the group G, and let a,b be
elements of G. Then the following conditions are equivalent:
- (1) bH = aH;
- (2) bH
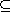 aH; aH;
- (3) b
 aH; aH;
- (4) a-1b
 H. H.
A result similar to Proposition 3.8.1 holds for right cosets. Let H be a
subgroup of the group G, and let a,b G.
Then the following conditions are equivalent: G.
Then the following conditions are equivalent:
- (1) Ha = Hb; (2) Ha
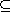 Hb;
(3) a Hb;
(3) a  Hb;
(4) ab-1 Hb;
(4) ab-1
 H; H;
- (5) ba-1
 H; (6) b H; (6) b
 Ha; (7)
Hb Ha; (7)
Hb 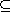 Ha.
Ha.
The index of H in G could also be defined as the number of right cosets of H in
G, since there is a one-to-one correspondence between left cosets and right
cosets.
3.7.5. Definition A subgroup H of the group G is called a normal
subgroup if
ghg-1
 H H
for all h  H
and g H
and g  G. G.
3.8.7. Proposition Let H be a subgroup of the group G. The following
conditions are equivalent:
- (1) H is a normal subgroup of G;
- (2) aH = Ha for all a
 G; G;
- (3) for all a,b
 G, abH is
the set theoretic product (aH)(bH); G, abH is
the set theoretic product (aH)(bH);
- (4) for all a,b
 G, ab-1 G, ab-1
 H if and
only if a-1b H if and
only if a-1b
 H. H.
Example 3.8.7. Any subgroup of index 2 is normal.
Factor groups
3.8.3. Proposition Let N be a normal subgroup of G, and let a,b,c,d
 G. G.
If aN = cN and bN = dN, then abN = cdN.
3.8.4. Theorem If N is a normal subgroup of G, then the set of left
cosets of N forms a group under the coset multiplication given by
aNbN = abN
for all a,b  G.
G.
3.8.5. Definition If N is a normal subgroup of G, then the group of
left cosets of N in G is called the factor group of G determined by N. It
will be denoted by G/N.
Example 3.8.5. Let N be a normal subgroup of G. If a
 G, then the
order of aN in G/N is the smallest positive integer n such that an G, then the
order of aN in G/N is the smallest positive integer n such that an
 N. N.
Group homomorphisms
3.7.1. Definition Let G1 and G2 be groups, and let
 : G1
-> G2 be a function. Then : G1
-> G2 be a function. Then
 is said to
be a group homomorphism if is said to
be a group homomorphism if
 (ab) = (ab) =
 (a) (a)
 (b) for all
a,b (b) for all
a,b  G1. G1.
Example 3.7.1. (Exponential functions for groups) Let G be any group, and
let a be any element of G. Define
 : Z
-> G by : Z
-> G by  (n)
= an, for all n (n)
= an, for all n
 Z.
This is a group homomorphism from Z to G. Z.
This is a group homomorphism from Z to G.
If G is abelian, with its operation denoted additively, then we define
 : Z
-> G by : Z
-> G by  (n)
= na. (n)
= na.
Example 3.7.2. (Linear transformations) Let V and W be vector spaces.
Since any vector space is an abelian group under vector addition, any linear
transformation between vector spaces is a group homomorphism.
3.7.2. Proposition If
 : G1
-> G2 is a group homomorphism, then : G1
-> G2 is a group homomorphism, then
- (a)
 (e) =
e; (e) =
e;
- (b) (
 (a))-1
= (a))-1
=  (a-1)
for all a (a-1)
for all a  G
1; G
1;
- (c) for any integer n and any a
 G1,
we have G1,
we have  (an)
= ( (an)
= ( (a))n; (a))n;
- (d) if a
 G1
and a has order n, then the order of G1
and a has order n, then the order of
 (a) in
G2 is a divisor of n. (a) in
G2 is a divisor of n.
Example 3.7.4. (Homomorphisms defined on cyclic groups) Let C be a cyclic
group, denoted multiplicatively, with generator a. If
 : C -> G
is any group homomorphism, and : C -> G
is any group homomorphism, and
 (a) = g,
then the formula (a) = g,
then the formula
 (am)
= gm must hold. Since every element of C is of the form am
for some integer m, this means that (am)
= gm must hold. Since every element of C is of the form am
for some integer m, this means that
 is
completely determined by its value on a. is
completely determined by its value on a.
If C is infinite, then for an element g of any group G, the formula
 (am)
= gm defines a homomorphism. (am)
= gm defines a homomorphism.
If |C|=n and g is any element of G whose order is a divisor of n, then the
formula  (am)
= gm defines a homomorphism. (am)
= gm defines a homomorphism.
Example 3.7.5. (Homomorphisms from Zn to Zk)
Any homomorphism
 : Zn
-> Zk is completely determined by : Zn
-> Zk is completely determined by
 ([1]n),
and this must be an element [m]k of Zk whose order
is a divisor of n. Then the formula ([1]n),
and this must be an element [m]k of Zk whose order
is a divisor of n. Then the formula
 ([x]n)
= [mx]k, for all [x]n ([x]n)
= [mx]k, for all [x]n
 Zn,
defines a homomorphism. Furthermore, every homomorphism from Zn
into Zk must be of this form. The image Zn,
defines a homomorphism. Furthermore, every homomorphism from Zn
into Zk must be of this form. The image
 (Zn)
is the cyclic subgroup generated by [m]k. (Zn)
is the cyclic subgroup generated by [m]k.
3.7.3 Definition Let
 : G1
-> G2 be a group homomorphism. Then : G1
-> G2 be a group homomorphism. Then
{ x
 G1
| G1
|  (x) = e } (x) = e }
is called the kernel of
 , and is
denoted by ker( , and is
denoted by ker( ). ).
3.7.4 Proposition Let
 : G1
-> G2 be a group homomorphism, with K = ker( : G1
-> G2 be a group homomorphism, with K = ker( ). ).
- (a) K is a normal subgroup of G.
- (b) The homomorphism
 is
one-to-one if and only if K = {e}. is
one-to-one if and only if K = {e}.
3.7.6 Proposition Let
 : G1
-> G2 be a group homomorphism. : G1
-> G2 be a group homomorphism.
- (a) If H1 is a subgroup of G1, then
 (H1)
is a subgroup of G2. (H1)
is a subgroup of G2.
If  is
onto and H1 is normal in G1, then is
onto and H1 is normal in G1, then
 (H1)
is normal in G2. (H1)
is normal in G2.
- (b) If H2 is a subgroup of G2, then
 -1
(H2) = { x -1
(H2) = { x
 G1
| G1
|  (x) (x)
 H2
} H2
}
is a subgroup of G1.
If H2 is normal in G2, then
 -1(H2)
is normal in G1. -1(H2)
is normal in G1.
3.8.6. Proposition Let N be a normal subgroup of G.
- (a) The natural projection mapping
 : G ->
G/N defined by : G ->
G/N defined by
 (x) = xN,
for all x (x) = xN,
for all x  G, is a homomorphism, and ker(
G, is a homomorphism, and ker( )
= N. )
= N.
- (b) There is a one-to-one correspondence between subgroups of G/N
and subgroups of G that contain N. Under this correspondence, normal
subgroups correspond to normal subgroups.
Example 3.8.8. If m is a divisor of n, then Zn / mZn
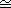 Zm. Zm.
3.8.8. Theorem [Fundamental Homomorphism Theorem] Let G1, G2
be groups.
If  : G1
-> G2 is a group homomorphism with K = ker( : G1
-> G2 is a group homomorphism with K = ker( ),
then ),
then
G1/K
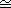
 (G1). (G1).
3.8.9. Definition The group G is called a simple group if it has
no proper nontrivial normal subgroups.
|

