The Galois group of a polynomial
To study solvability by radicals of a polynomial equation f(x) = 0, we let K be
the field generated by the coefficients of f(x), and let F be a splitting field
for f(x) over K. Galois considered permutations of the roots that leave the
coefficient field fixed. The modern approach is to consider the automorphisms
determined by these permutations. We note that any automorphism of a field F
must leave its prime subfield fixed.
8.1.1. Proposition. Let F be an extension field of K. The set of all
automorphisms  : F -> F such that
: F -> F such that
 (a) = a for
all a in K is a group under composition of functions. (a) = a for
all a in K is a group under composition of functions.
8.1.2. Definition. Let F be an extension field of K. The set
{
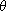
 Aut(F) | Aut(F) |
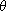 (a) = a
for all a (a) = a
for all a  K } K }
is called the Galois group of F over K, denoted by Gal(F/K).
8.1.3. Definition. Let K be a field, let f(x)
 K[x], and let
F be a splitting field for f(x) over K. Then Gal(F/K) is called the Galois
group of f(x) over K, or the Galois group of the equation f(x) = 0 over K. K[x], and let
F be a splitting field for f(x) over K. Then Gal(F/K) is called the Galois
group of f(x) over K, or the Galois group of the equation f(x) = 0 over K.
8.1.4. Proposition. Let F be an extension field of K, and let f(x)
 K[x]. Then
any element of Gal(F/K) defines a permutation of the roots of f(x) that lie in
F. K[x]. Then
any element of Gal(F/K) defines a permutation of the roots of f(x) that lie in
F.
8.1.5. Lemma. Let f(x)
 K[x] be a
polynomial with no repeated roots and let F be a splitting field for f(x) over
K. If K[x] be a
polynomial with no repeated roots and let F be a splitting field for f(x) over
K. If  : K ->
L is a field isomorphism that maps f(x) to g(x) : K ->
L is a field isomorphism that maps f(x) to g(x)
 L[x] and E is
a splitting field for g(x) over L, then there exist exactly [F:K] isomorphisms L[x] and E is
a splitting field for g(x) over L, then there exist exactly [F:K] isomorphisms
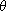 : F -> E
such that : F -> E
such that 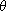 (a) =
(a) =  (a)
for all a in K. (a)
for all a in K.
8.1.6. Theorem. Let K be a field, let f(x)
 K[x], and let
F be a splitting field for f(x) over K. If f(x) has no repeated roots, then
|Gal(F/K)| = [F:K]. K[x], and let
F be a splitting field for f(x) over K. If f(x) has no repeated roots, then
|Gal(F/K)| = [F:K].
8.1.7. Corollary. Let K be a finite field and let F be an extension of
K with [F:K] = m. Then Gal(F/K) is a cyclic group of order m.
Multiplicity of roots
8.2.1. Definition. Let f(x) be a polynomial in K[x], and let F be a
splitting field for f(x) over K. If f(x) has the factorization
f(x) = (x - r1)m1 (x - r2)m2
� � � (x - rt)mt
over F, then we say that the root ri has multiplicity mi.
If mi=1, then ri is called a simple root.
8.2.2. Definition. Let f(x)
 K[x], with
f(x) = K[x], with
f(x) = 
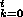 ak
xk. The formal derivative f'(x) of f(x) is defined by the
formula ak
xk. The formal derivative f'(x) of f(x) is defined by the
formula
f'(x) =

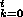 k ak
xk-1, k ak
xk-1,
where k ak denotes the sum of ak added to itself k times.
8.2.3. Proposition. The polynomial f(x) in K[x] has no multiple roots
if and only if gcd(f(x),f'(x)) = 1.
8.2.4. Proposition. Let f(x) be an irreducible polynomial over the
field K. Then f(x) has no multiple roots unless chr(K) = p
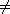 0 and f(x)
has the form 0 and f(x)
has the form
f(x) = a0 + a1 xp + a2
x2p + � � � + an xnp.
8.2.5. Definition. A polynomial f(x) over the field K is called
separable if its irreducible factors have only simple roots.
An algebraic extension field F of K is called separable over K if the
minimal polynomial of each element of F is separable.
The field F is called perfect if every polynomial over F is separable.
8.2.6. Theorem. Any field of characteristic zero is perfect. A field
of characteristic p>0 is perfect if and only if each of its elements has a pth
root.
8.2.7. Corollary. Any finite field is perfect.
8.2.8. Theorem. Let F be a finite extension of the field K. If F is
separable over K, then it is a simple extension of K.
The fundamental theorem of Galois theory
8.3.1. Proposition. Let F be a field, and let G be a subgroup of Aut(F).
Then
{ a
 F | F |
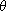 (a) = a
for all (a) = a
for all 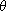
 G } G }
is a subfield of F.
8.3.2. Definition. Let F be a field, and let G be a subgroup of Aut
(F). Then
{ a
 F | F |
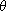 (a) = a
for all (a) = a
for all 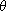
 G } G }
is called the G-fixed subfield of F, or the G-invariant subfield
of F, and is denoted by FG.
8.3.3. Proposition. If F is the splitting field over K of a separable
polynomial and G = Gal(F/K), then FG = K.
8.3.4. Lemma. [Artin] Let G be a finite group of automorphisms of the
field F, and let K = FG. Then
[F:K]
 | G |. | G |.
8.3.5. Definition. Let F be an algebraic extension of the field K. Then F
is said to be a normal extension of K if every irreducible polynomial in
K[x] that contains a root in F is a product of linear factors in F[x].
8.3.6. Theorem. The following conditions are equivalent for an
extension field F of K:
- (1) F is the splitting field over K of a separable polynomial;
- (2) K = FG for some finite group G of automorphisms of
F;
- (3) F is a finite, normal, separable extension of K.
8.3.7. Corollary. If F is an extension field of K such that K = FG
for some finite group G of automorphisms of F, then G = Gal(F/K).
Example. 8.3.1. The Galois group of GF(pn) over GF(p) is
cyclic of order n, generated by the automorphism
 defined by defined by
 (x) = xp,
for all x in GF(pn). This automorphism is usually known as the
Frobenius automorphism of GF(pn). (x) = xp,
for all x in GF(pn). This automorphism is usually known as the
Frobenius automorphism of GF(pn).
8.3.8. Theorem. [Fundamental Theorem of Galois Theory] Let F be the
splitting field of a separable polynomial over the field K, and let G =
Gal(F/K).
- (a) There is a one-to-one order-reversing correspondence between
subgroups of G and subfields of F that contain K:
- (i) If H is a subgroup of G, then the corresponding subfield is FH,
and
H = Gal(F/FH).
- (ii) If E is a subfield of F that contains K, then the corresponding
subgroup of G is H = Gal(F/E), and
E = FH.
- (b) For any subgroup H of G, we have
[F:FH] = | H | and [FH:K] = [G:H].
- (c) Under the above correspondence, the subgroup H is normal if
and only if the subfield E = FH is a normal extension of K. In
this case,
Gal(E/K)
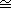 Gal(F/K)
/ Gal(F/E). Gal(F/K)
/ Gal(F/E).
In the statement of the fundamental theorem we could have simply said that
normal subgroups correspond to normal extensions. In the proof we noted that if
E is a normal extension of K, then
 (E) (E)
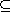 E for
all E for
all  in
Gal(F/K). In the context of the fundamental theorem, we say that two
intermediate subfields E1 and E2 are conjugate if
there exists in
Gal(F/K). In the context of the fundamental theorem, we say that two
intermediate subfields E1 and E2 are conjugate if
there exists 
 Gal(F/K) such
that Gal(F/K) such
that  ( E1
) = E2. We now show that the subfields conjugate to an intermediate
subfield E correspond to the subgroups conjugate to Gal(F/E). Thus E is a normal
extension if and only if it is conjugate only to itself. ( E1
) = E2. We now show that the subfields conjugate to an intermediate
subfield E correspond to the subgroups conjugate to Gal(F/E). Thus E is a normal
extension if and only if it is conjugate only to itself.
8.3.9. Proposition. Let F be the splitting field of a separable
polynomial over the field K, and let E be a subfield such that K
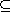 E E
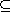 F, with
H = Gal(F/E). If F, with
H = Gal(F/E). If

 Gal(F/K),
then Gal(F/K),
then
Gal(F/ (E))
= (E))
=  H H
 -1. -1.
8.3.10. Theorem. [Fundamental Theorem of Algebra] Any polynomial in C[x]
has a root in C.
Solvability by radicals
In most results in this section we will assume that the fields have
characteristic zero, in order to guarantee that no irreducible polynomial has
multiple roots. When we say that a polynomial equation is solvable by radicals,
we mean that the solutions can be obtained from the coefficients in a finite
sequence of steps, each of which may involve addition, subtraction,
multiplication, division, or taking nth roots. Only the extraction of
an nth root leads to a larger field, and so our formal definition is
phrased in terms of subfields and adjunction of roots of xn-a for
suitable elements a.
8.4.1. Definition. An extension field F of K is called a radical
extension of K if there exist elements u1, u2, ... , um
in F such that
- (i) F = K (u1, u2, ... , um),
and
- (ii) u1n1
 K and uini K and uini
 K ( u1,
... , ui-1 ) for i = 2, ... , m and n1, n2,
... , nm K ( u1,
... , ui-1 ) for i = 2, ... , m and n1, n2,
... , nm
 Z. Z.
For f(x)  K[x], the polynomial equation f(x) = 0 is said to be solvable by radicals
if there exists a radical extension F of K that contains all roots of f(x).
K[x], the polynomial equation f(x) = 0 is said to be solvable by radicals
if there exists a radical extension F of K that contains all roots of f(x).
8.4.2. Proposition. Let F be the splitting field of xn - 1
over a field K of characteristic zero. Then Gal(F/K) is an abelian group.
8.4.3. Theorem. Let K be a field of characteristic zero that contains
all nth roots of unity, let a
 K, and let F
be the splitting field of xn-a over K. Then Gal(F/K) is a cyclic
group whose order is a divisor of n. K, and let F
be the splitting field of xn-a over K. Then Gal(F/K) is a cyclic
group whose order is a divisor of n.
8.4.4. Theorem. Let p be a prime number, let K be a field that
contains all pth roots of unity, and let F be an extension of K. If
[F:K] = |Gal(F/K)| = p, then F = K(u) for some u
 F such that up F such that up
 K. K.
8.4.5. Lemma. Let K be a field of characteristic zero, and let E be a
radical extension of K. Then there exists an extension F of E that is a normal
radical extension of K.
8.4.6. Theorem. Let f(x) be a polynomial over a field K of
characteristic zero. The equation f(x) = 0 is solvable by radicals if and only
if the Galois group of f(x) over K is solvable.
Theorem
7.7.2 shows that Sn is not solvable for n
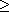 5, and so to
give an example of a polynomial equation of degree n that is not solvable by
radicals, we only need to find a polynomial of degree n whose Galois group over
Q is Sn. 5, and so to
give an example of a polynomial equation of degree n that is not solvable by
radicals, we only need to find a polynomial of degree n whose Galois group over
Q is Sn.
8.4.7. Lemma. Any subgroup of S5 that contains both a
transposition and a cycle of length 5 must be equal to S5 itself.
8.4.8. Theorem. There exists a polynomial of degree 5 with rational
coefficients that is not solvable by radicals.
Cyclotomic polynomials
8.5.1. Definition. Let n be a positive integer, and let
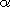 be the
complex number be the
complex number
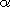 = cos = cos
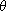 + i sin + i sin
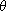 , where , where
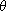 = 2 = 2
 / n. The
polynomial / n. The
polynomial
 n
(x) = n
(x) =  k
(x - k
(x - 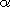 k), k),
where k belongs to the set of positive integers less than n and relatively prime
to n, is called the nth cyclotomic polynomial.
8.5.2. Proposition. Let n be a positive integer, and let
 n(x)
be the nth cyclotomic polynomial. The following conditions hold: n(x)
be the nth cyclotomic polynomial. The following conditions hold:
- (a) deg (
 n
(x)) = n
(x)) = 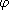 (n);
(n);
- (b) xn - 1 =
 d
| n d
| n  d
(x); d
(x);
- (c)
 n
(x) is monic, with integer coefficients. n
(x) is monic, with integer coefficients.
8.5.3. Theorem. The nth cyclotomic polynomial
 n(x)
is irreducible over Q, for every positive integer n. n(x)
is irreducible over Q, for every positive integer n.
8.5.4. Theorem. For every positive integer n, the Galois group of the
nth cyclotomic polynomial
 n(x)
over Q is isomorphic to Zn�. n(x)
over Q is isomorphic to Zn�.
Example. 8.5.2. A regular n-gon is constructible if and only if
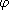 (n) is a
power of 2. If p is an odd prime, and (n) is a
power of 2. If p is an odd prime, and
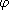 (p) is a
power of 2, then p must have the form p = 2k + 1, where k is a power
of 2. Such primes are called Fermat primes. The only known examples are
3, 5, 17, 257, and 65537. This implies, for example, that a regular 17-gon is
constructible. (p) is a
power of 2, then p must have the form p = 2k + 1, where k is a power
of 2. Such primes are called Fermat primes. The only known examples are
3, 5, 17, 257, and 65537. This implies, for example, that a regular 17-gon is
constructible.
A set that satisfies all the axioms of a field except for commutativity of
multiplication is called a division ring or skew field.
8.5.6. Theorem. [Wedderburn] Any finite division ring is a field.
Computing Galois groups
8.6.1. Definition. Let G be a group acting on a set S. We say that G acts
transitively on S if for each pair of elements x,y in S there exist an
element g in G such that y = gx.
If G is a subgroup of the symmetric group Sn, then G is called a
transitive group if it acts transitively on the set { 1, 2, ... , n }.
8.6.2. Proposition. Let f(x) be a separable polynomial over the field
K, with roots r1 , ... , rn in its splitting field F. Then
f(x) is irreducible over K if and only if Gal(F/K) acts transitively on the
roots of f(x).
8.6.3. Lemma. Let p be a prime number, and let G be a transitive
subgroup of Sp. Then any nontrivial normal subgroup of G is also
transitive.
8.6.4. Lemma. Let p be a prime number, and let G be a solvable,
transitive subgroup of Sp. Then G contains a cycle of length p.
8.6.5. Proposition. Let p be a prime number, and let G be a solvable,
transitive subgroup of Sp. Then G is a subgroup of the normalizer in
Sp of a cyclic subgroup of order p.
Let f(x) be a polynomial of degree n over the field K, and assume that f(x)
has roots r1, r2, ... , rn in its splitting
field F. The element
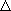 of F
defined by of F
defined by
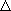 = =
 (ri
- rj)2, (ri
- rj)2,
where the product is taken over all i,j with 1
 i < j i < j
 n, is called
the discriminant of f(x). n, is called
the discriminant of f(x).
It can be shown that the discriminant of any polynomial f(x) can be expressed
as a polynomial in the coefficients of f(x), with integer coefficients. This
requires use of elementary symmetric functions, and lies beyond the scope of
what we have chosen to cover in the book.
We have the following properties of the discriminant:
- (i)
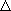
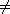 0 if and
only if f(x) has distinct roots; 0 if and
only if f(x) has distinct roots;
- (ii)
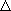
 K; K;
- (iii) If
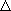
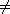 0, then
a permutation 0, then
a permutation

 Sn
is even if and only if it leaves unchanged the sign of Sn
is even if and only if it leaves unchanged the sign of

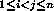 (ri-rj)
. (ri-rj)
.
8.6.6. Proposition. Let f(x) be a separable polynomial over the field K,
with discriminant
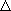 , and let F
be its splitting field over K. Then every permutation in Gal(F/K) is even if and
only if , and let F
be its splitting field over K. Then every permutation in Gal(F/K) is even if and
only if 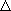 is
the square of some element in K. is
the square of some element in K.
We now restrict our attention to polynomials with rational coefficients. The
next lemma shows that in computing Galois groups it is enough to consider
polynomials with integer coefficients. Then a powerful technique is to reduce
the integer coefficients modulo a prime and consider the Galois group of the
reduced equation over the field GF(p).
8.6.7. Lemma. Let f(x) = xn + an-1 xn-1
+ � � � + a1 x + a0
 Q[x],
and assume that Q[x],
and assume that
ai = bi / d for d, b0, b1, ... , bn-1
 Z. Z.
Then dn f(x/d) is monic with integer coefficients, and has the same
splitting field over Q as f(x).
If p is a prime number, we have the natural mapping
 : Z[x]
-> Zp[x] which reduces each coefficient modulo p. We will use
the notation : Z[x]
-> Zp[x] which reduces each coefficient modulo p. We will use
the notation  (
f(x) ) = fp(x). (
f(x) ) = fp(x).
Theorem [Dedekind]. Let f(x) be a monic polynomial of degree n, with
integer coefficients and Galois group G over Q, and let p be a prime such
that fp(x) has distinct roots. If fp(x) factors in Zp[x]
as a product of irreducible factors of degrees n1, n2, ...
, nk, then G contains a permutation with the cycle decomposition
(1,2, ... ,n1) (n1+1, n1+2,
... , n1+n2) � � � (n-nk+1, ... ,n),
relative to a suitable ordering of the roots.
|

