Dedekind domains
In this section we investigate a new approach to unique factorization, using
ideals rather than elements. If D is a principal ideal domain, then any nonzero
ideal I of D has the form I= aD for some nonzero a
 D with a = p1p2
. . . pn for irreducible elements p1, p2,
. . . , pn of D. It follows that I is a product of prime ideals,
since aD = D with a = p1p2
. . . pn for irreducible elements p1, p2,
. . . , pn of D. It follows that I is a product of prime ideals,
since aD =
 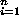 piD. We use this condition as our definition of a Dedekind domain.
piD. We use this condition as our definition of a Dedekind domain.
12.1.1. Definition. An integral domain D is called a Dedekind
domain if each proper ideal of D can be written as a product of a finite
number of prime ideals of D.
We will show in
Theorem
12.2.4 that a Dedekind domain has some of the properties of a principal
ideal domain. Specifically, a Dedekind domain must be Noetherian, and any
nonzero prime ideal of a Dedekind domain must be maximal. This shows that a
unique factorization domain can fail to be a Dedekind domain, since, for
example, the unique factorization domain Q[x,y] contains the
nonzero prime ideals <x>
 <x,y>. <x,y>.
We will prove a number of facts about Dedekind domains by using the notion of
an ``inverse'' of an ideal. This necessitates the introduction of the following
concept.
12.1.2. Definition. Let D be an integral domain with quotient field F.
A fractional ideal of D is a nonzero D-submodule I of F such that there
exists 0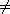 d d
 D with dI D with dI
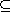 D. D.
If I is a fractional ideal of D, we define
I-1 = { q
 F | qI F | qI
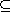 D }, D },
and say that I is invertible if I-1I = D.
12.1.3. Lemma. Let D be an integral domain with quotient field F, and
let I be an ideal of D that is invertible when considered as a fractional ideal.
The following conditions hold.
(a) The ideal I is finitely generated.
(b) If I is a product of prime ideals, then this product is unique (up to
order).
12.1.4. Theorem. The following conditions hold for any Dedekind domain
D.
(a) Every nonzero ideal of D is invertible.
(b) Every proper ideal of D can be written uniquely (up to order) as a
product of a finite number of prime ideals of D;
(c) D is a Noetherian domain.
(d) Every nonzero prime ideal of D is maximal.
12.1.5. Proposition. Let D be an integral domain. A fractional ideal I
of D is invertible if and only if it is projective as a D-module.
12.1.6. Theorem. The following conditions are equivalent for an
integral domain D.
(1) D is a Dedekind domain;
(2) every nonzero ideal of D is invertible;
(3) every fractional ideal of D is invertible;
(4) every nonzero ideal of D is projective as a D-module.
12.1.7. Proposition. Let D be an integral domain with quotient field
F. Assume that D is Noetherian and that every nonzero prime ideal of D is
maximal. Then for any proper nonzero ideal I of D there exists q
 F-D with qI F-D with qI
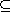 D. D.
Integral extensions
We recall that an extension field F
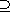 K in
which each element is a root of a nonzero polynomial with coefficients in K is
said to be algebraic over K. There is a similar concept for ring extensions T K in
which each element is a root of a nonzero polynomial with coefficients in K is
said to be algebraic over K. There is a similar concept for ring extensions T
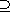 R,
which reduces to the familiar one for fields. R,
which reduces to the familiar one for fields.
12.2.1. Definition. Let R be a subring of the commutative ring T. An
element u  T
is said to be integral over R if there exists a monic polynomial f(x) T
is said to be integral over R if there exists a monic polynomial f(x)
 R[x] such
that f(u)=0. R[x] such
that f(u)=0.
The ring T is said to be an integral extension of R if each element of T
is integral over R.
12.2.2. Proposition. Let R be a subring of the commutative ring T. The
following conditions are equivalent for an element u
 T. T.
(1) u is integral over R;
(2) the subring R[u] generated by R and u is finitely generated as an
R-module;
(3) there exists a subring R' with R
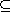 R' R'
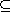 T such
that R[u] T such
that R[u]
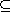 R' and
R' is finitely generated as an R-module; R' and
R' is finitely generated as an R-module;
(4) there exists a faithful R[u]-submodule of T that is finitely
generated as an R-module.
12.2.3. Corollary. Let R be a subring of the commutative ring T. If T
is finitely generated as a module over R, then T is an integral extension of R.
12.2.4. Corollary. Let R be a subring of the commutative ring T. Then
R* = { u  T |
u is integral over R } T |
u is integral over R }
is a subring of T.
12.2.5. Definition. Let R be a subring of the commutative ring T. The
subring R* of all elements integral over R is called the integral closure
of R in T.
If R* = R, then we say that R is integrally closed in T. If D is an
integral domain that is integrally closed in its quotient field, then we simply
say that D is integrally closed.
12.2.6. Proposition. Let R be a subring of the integral domain D, and
assume that D is an integral extension of R. Then D is a field if and only if R
is a field.
12.2.7. Corollary. Let R be a subring of the commutative ring T, and
assume that T is an integral extension of R. If Q is a prime ideal of T, then Q
is a maximal ideal of T if and only if Q R
is a maximal ideal of R. R
is a maximal ideal of R.
12.2.8. Proposition. Let R be a subring of the integral domain D, and
assume that D is an integral extension of R. If S is any multiplicative set of
R, then DS is an integral extension of RS.
12.2.9. Theorem. Let R be a subring of the integral domain D, and
assume that D is an integral extension of R.
(a) (Incomparability) Let Q, Q' be prime ideals of D such that Q
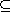 Q '.
Then Q Q '.
Then Q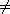 Q'
implies Q Q'
implies Q  R R
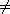 Q' Q'
 R. R.
(b) (Lying-over) For each prime ideal P of R there exists a prime ideal Q
of D such that Q
 R = P. R = P.
(c) (Going up) If P
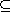 P' are
prime ideals of R, and Q is a prime ideal of D with Q P' are
prime ideals of R, and Q is a prime ideal of D with Q
 R = P, then
there exists a prime ideal Q' of D such that Q R = P, then
there exists a prime ideal Q' of D such that Q
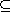 Q' and
Q' Q' and
Q'  R = P'. R = P'.
In the setting of the previous theorem, if we assume in addition that R is an
integrally closed domain, then a further condition holds, known as ``Going
down'': Let R be a subring of the integral domain D, assume that D is an
integral extension of R, and that R is an integrally closed domain. If P'
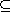 P are
prime ideals of R, and Q is a prime ideal of D with Q P are
prime ideals of R, and Q is a prime ideal of D with Q R
= P, then there exists a prime ideal Q' of D such that Q' R
= P, then there exists a prime ideal Q' of D such that Q'
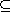 Q and
Q' Q and
Q' R = P'. R = P'.
12.2.10. Theorem. The following conditions are equivalent for an
integral domain D.
(1) D is a Dedekind domain;
(2) D is Noetherian, integrally closed in its quotient field, and each
nonzero prime ideal of D is maximal.
12.2.11. Theorem. Let D be an integral domain with quotient field Q,
and let F be a finite extension field of Q. If D* is the set of all elements of
F that are integral over D, then D* is a Dedekind domain.
Let p be a prime, and let
 be a
primitive pth root of unity. If Z[ be a
primitive pth root of unity. If Z[ ]
denotes the subring of C generated by ]
denotes the subring of C generated by
 , then it
can be shown that Z[ , then it
can be shown that Z[ ]
is the integral closure of Z in Q( ]
is the integral closure of Z in Q( ),
the splitting field over Q of xp-1. It follows that
Z[ ),
the splitting field over Q of xp-1. It follows that
Z[ ]
is a Dedekind domain. ]
is a Dedekind domain.
Primary decomposition
Let F be a field, and first consider the ring F[x] of polynomials in one
indeterminate. Since this ring is a principal ideal domain, each ideal is a
product of prime ideals. Unfortunately, although the ring F[x,y] of polynomials
in two indeterminates is a unique factorization domain, the ideal structure is
not so simple. For an example that illustrates this particular difficulty,
consider the ideal <x2,y> generated by the elements x2 and
y. In F[x,y]/<y>
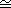 F[x], the
only prime ideal that contains <x2,y>/<y> is <x,y>/<y>. It follows
that in F[x,y] the only prime ideal that contains <x2,y> is <x,y>.
Since <x,y>2=<x2,xy,y2>, which is properly
contained in <x2,y>, it is impossible to express <x2,y> as
a product of prime ideals. F[x], the
only prime ideal that contains <x2,y>/<y> is <x,y>/<y>. It follows
that in F[x,y] the only prime ideal that contains <x2,y> is <x,y>.
Since <x,y>2=<x2,xy,y2>, which is properly
contained in <x2,y>, it is impossible to express <x2,y> as
a product of prime ideals.
To obtain an appropriate generalization of unique factorization of ideals in
polynomial rings, it is necessary to replace products of ideals with
intersections of ideals, and to replace powers of prime ideals with ``primary''
ideals. The primary decomposition theorem does not depend on having unique
factorization of elements, but simply on having the ascending chain condition on
ideals, so it remains true for all Noetherian rings.
12.3.1. Proposition. Let R be a commutative ring. The set of all
nilpotent elements of R forms an ideal of R.
12.3.2. Definition. Let R be a commutative ring. The nil radical
of R is defined to be the ideal
N(R) = { x  R
| xn = 0 for some n R
| xn = 0 for some n
 Z+
}. Z+
}.
12.3.3. Theorem. Let R be a commutative ring.
(a) The nil radical of R / N(R) is zero.
(b) The nil radical of R is the intersection of all prime ideals of R.
The ideal N(R) is also called the prime radical of R. This terminology
is justified by the above theorem. This definition can be extended to
noncommutative rings, where the prime radical of R is defined to be the
intersection of all prime ideals of R.
12.3.4. Definition. Let R be a commutative ring, and let I be an ideal
of R. The ideal
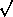 I = { x I = { x
 R | xn R | xn
 I for some n I for some n
 Z+
} Z+
}
is called the radical of I.
We note that if I is an ideal of R, then
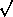 I is the
inverse image in R of the nil radical of R/I, which shows that I is the
inverse image in R of the nil radical of R/I, which shows that
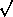 I is an
ideal. It also follows that I is an
ideal. It also follows that
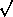 I is the
intersection of all prime ideals of R that contain I. I is the
intersection of all prime ideals of R that contain I.
In any principal ideal domain, our next definitions both reduce to the
statement that the ideal in question is generated by a power of an irreducible
element. But even for the polynomial ring in two indeterminates over a field or
the ring of polynomials with integer coefficients the two concepts are distinct.
12.3.5. Definition. Let I be an ideal of the commutative ring R.
We say that I is a primary ideal if for all elements a,b
 R we have the
following condition: R we have the
following condition:
ab  I implies
a I implies
a  I or bn I or bn
 I, for some n I, for some n
 Z+. Z+.
We say that I is an irreducible ideal if
I = J K
implies I=J or I=K, K
implies I=J or I=K,
for all ideals J,K of R with I
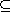 J and I J and I
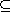 K. K.
Let D be a principal ideal domain, let p be an irreducible element D, and let
Q=pnD. If a,b
 D with ab D with ab
 Q, then pn|ab,
so either p|a or p|b. If a Q, then pn|ab,
so either p|a or p|b. If a
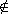 I, then p I, then p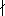 a
implies pn|b, and hence b a
implies pn|b, and hence b
 Q. This shows
that Q is a primary ideal. Q. This shows
that Q is a primary ideal.
Note that if I,Q are ideals of R with I
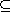 Q, then
Q is a primary ideal of R if and only if Q/I is a primary ideal of R/I. If F is
any field, we can apply this observation to R=F[x,y], Q=<x2,y>, and
I=<y> to show that <x2,y> is a primary ideal of F[x,y]. This provides
an example of a primary ideal that is not a power of a prime ideal. Q, then
Q is a primary ideal of R if and only if Q/I is a primary ideal of R/I. If F is
any field, we can apply this observation to R=F[x,y], Q=<x2,y>, and
I=<y> to show that <x2,y> is a primary ideal of F[x,y]. This provides
an example of a primary ideal that is not a power of a prime ideal.
12.3.6. Proposition. Let R be a commutative Noetherian ring. Then
every irreducible ideal of R is a primary ideal.
12.3.7. Lemma. Let R be a commutative ring.
(a) If I is a primary ideal of R, then
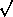 I is a
prime ideal of R. I is a
prime ideal of R.
(b) If { Qi }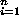 is a collection of primary ideals of R such that
is a collection of primary ideals of R such that
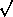 Qi=P
for 1 Qi=P
for 1  i i
 n, then n, then
 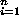 Qi is a primary ideal of R with
Qi is a primary ideal of R with
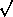 ( (
 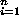 Qi ) = P.
Qi ) = P.
12.3.8. Definition. Let Q be a primary ideal of the commutative ring
R. We say that
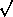 Q is the
associated prime ideal of Q. If P = Q is the
associated prime ideal of Q. If P =
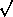 Q, then
we say that Q belongs to the prime ideal P and that Q is primary for
P. Q, then
we say that Q belongs to the prime ideal P and that Q is primary for
P.
12.3.10. Theorem. [Lasker-Noether Decomposition Theorem] Let R be a
commutative, Noetherian ring, and let I be an ideal of R.
There exist primary ideals { Qi }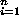 with I =
with I =  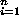 Qi, such that no Qi contains the intersection of the other
primary ideals, and the ideals Qi have distinct associated primes.
Qi, such that no Qi contains the intersection of the other
primary ideals, and the ideals Qi have distinct associated primes.
Furthermore, in any such representation of I as an intersection of primary
ideals, there must be n ideals, and the set of their associated prime ideals
must be the same.
Noetherian rings
We have shown that if R is any left Noetherian ring, then the ring R[x] of
polynomials with coefficients in R is again left Noetherian. This implies that
if R is any commutative Noetherian ring, then the polynomial ring R[x1,
x2, . . . , xn] is again Noetherian. The next example
provides another large class of Noetherian rings.
Example. 12.4.1. Let R be any commutative ring. We define the ring R
[[x]] of all formal power series over R as the set of all sequences a=(a0,
a1, a2, . . . ), with componentwise addition and a
multiplication given by defining
(a0, a1, a2, . . . ) . (b0,
b1, b2, . . . ) = (c0, c1, c2,
. . . ) ,
where ci =
 i=j+k
aj bk. i=j+k
aj bk.
It can be checked easily that R[[x]] is a ring, that R can be identified with
elements of the form (a0, 0, 0, . . . ), and that the polynomial ring
R[x] can be identified with the subset of all sequences with only finitely many
nonzero terms.
12.4.1. Theorem. [Cohen] Let R be a commutative ring. Then R is
Noetherian if and only if every prime ideal of R is finitely generated.
12.4.2. Corollary. If R is a commutative Noetherian ring, then so is
the ring R[[x]] of all formal power series over R.
12.4.3. Theorem. Let R be a commutative Noetherian ring. Then the nil
radical of R is nilpotent. That is, there exists m
 Z+
such that N(R)m=(0). Z+
such that N(R)m=(0).
12.4.4. Corollary. If Q is a primary ideal of the commutative
Noetherian ring R, then there exists a positive integer m such that (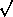 Q)m Q)m
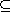 Q. Q.
12.4.5. Lemma. Let J be an ideal of the commutative Noetherian ring R,
and let I =
 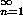 Jn. Then JI = I.
Jn. Then JI = I.
12.4.6. Theorem. [Krull] Let R be a commutative Noetherian ring. Then
the intersection of powers of the Jacobson radical is zero. That is,
 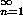 (J(R))n=(0), where J(R) is the Jacobson radical of R.
(J(R))n=(0), where J(R) is the Jacobson radical of R.
We now state several results whose proofs are beyond the scope of this brief
introduction to Noetherian rings. Recall that in a principal ideal domain every
nonzero prime ideal is maximal, so that the only proper chains of prime ideals
have the form P
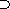 (0). This
result was extended by Krull to Noetherian rings, and is known as the principal
ideal theorem: If R is a Noetherian ring, aR is a proper principal ideal of R,
and P is any prime ideal minimal over aR, then P contains no chains of primes
longer than P (0). This
result was extended by Krull to Noetherian rings, and is known as the principal
ideal theorem: If R is a Noetherian ring, aR is a proper principal ideal of R,
and P is any prime ideal minimal over aR, then P contains no chains of primes
longer than P
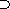 P1. P1.
We say that a chain P0
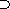 P1 P1
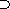 . . . . . .
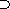 Pm
of prime ideals has length m. An induction argument can be used to generalize
the principal ideal theorem, and this important result is usually called Krull's
generalized principal ideal theorem. We will investigate some of its
consequences for the study of polynomial rings. Pm
of prime ideals has length m. An induction argument can be used to generalize
the principal ideal theorem, and this important result is usually called Krull's
generalized principal ideal theorem. We will investigate some of its
consequences for the study of polynomial rings.
12.4.7. Theorem. [Generalized principal ideal theorem] Let I be a
proper ideal of the Noetherian ring R. If I is generated by m elements, and P is
any prime ideal minimal over I, then any chain of primes
P 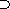 P1 P1
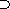 . . . has
length at most m. . . . has
length at most m.
One important consequence of the generalized principal ideal theorem is that
any Noetherian ring satisfies the descending chain condition for prime ideals.
There may or may not be a uniform bound on the lengths of chains of prime ideals
of a Noetherian ring. If R is Noetherian, and has a chain of prime ideals of
length n, but none longer, then we say that R has Krull dimension equal
to n.
A field F is said to be algebraically closed if every monic polynomial
of positive degree with coefficients in F has a root in F. As a second
consequence of the generalized principal ideal theorem, we can compute the Krull
dimension of the polynomial ring R=F[x1, x2, . . . , xn],
where F is algebraically closed. It can be shown that any maximal ideal of R is
generated by n elements x1-a1, x2-a2,
. . . , xn-an. It follows that any chain of prime ideals
of R has length at most n. Of course, there is a chain of length n, given by
< x1, x2, . . . , xn >
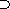 < x2,
. . . , xn > < x2,
. . . , xn >
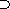 . . . . . .
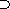 < xn
> < xn
> 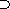 (0). (0).
Thus R has Krull dimension n.
12.4.8. Lemma. Let F be an algebraically closed field, and let f, f1,
. . . , fm be elements of the polynomial ring F[x1, . . .
, xn]. If the system
f(x1, . . . , xn)
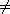 0 0
f1(x1, . . . , xn) = . . . = fm(x1,
. . . , xn) = 0
has a solution in some extension field of F, then it must have a solution in F.
12.4.9. Theorem. [Hilbert's Nullstellensatz] Let F be an algebraically
closed field, and let I be any ideal of the polynomial ring F[x1, . .
. , xn]. Then
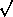 I
consists of all elements f I
consists of all elements f
 F[x1,
. . . , xn] such that f(a1, a2, . . . , an)
= 0 for all (a1, a2, . . . , an) such that g(a1,
a2, . . . , an) = 0 for all g F[x1,
. . . , xn] such that f(a1, a2, . . . , an)
= 0 for all (a1, a2, . . . , an) such that g(a1,
a2, . . . , an) = 0 for all g
 I. I.
|

