Divisors; prime factorization
The set {..., -2, -1, 0, 1, 2, 3, ...} is called the set of integers, and
will be denoted by Z.
1.1.1. Definition. An integer a is called a
multiple of an integer b if a=bq for some integer q. In this case we
also say that b is a divisor of a, and we use the
notation b | a.
In the above case we can also say that b is a factor
of a, or that a is divisible by b. If b is not a divisor of a, meaning
that a 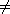 bq
for all q bq
for all q  Z, then we write b
Z, then we write b
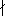 a. The set
of all multiples of an integer a will be denoted by a. The set
of all multiples of an integer a will be denoted by
aZ = { m
 Z |
m=aq for some q Z |
m=aq for some q
 Z }. Z }.
1.1.2. Axiom. [Well-Ordering Principle] Every nonempty set of natural
numbers contains a smallest element.
1.1.3 Theorem. [Division Algorithm] For any integers a and b, with
b>0, there exist unique integers q (the quotient) and r (the remainder)
such that a=bq+r, with 0
 r<b. r<b.
1.1.4. Theorem. Let I be a nonempty set of integers that is closed
under addition and subtraction. Then I either consists of zero alone or else
contains a smallest positive element, in which case I consists of all multiples
of its smallest positive element.
1.1.5. Definition. A positive integer d is called the greatest
common divisor of the nonzero integers a and b if
- (i) d is a divisor of both a and b, and
- (ii) any divisor of both a and b is also a divisor of d.
We will use the notation gcd(a,b), or simply (a,b), for the greatest common
divisor of a and b.
1.1.6. Theorem. Any two nonzero integers a and b have a greatest
common divisor, which can be expressed as the smallest positive linear
combination of a and b.
Moreover, an integer is a linear combination of a and b if and only if it is a
multiple of their greatest common divisor.
The greatest common divisor of two numbers can be computed by using a
procedure known as the Euclidean algorithm. First,
note that if a
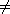 0 and b | a,
then gcd(a,b) = |b|. The next observation provides the basis for the Euclidean
algorithm. If a=bq+r, then (a,b)=(b,r). Thus given integers a>b>0, the Euclidean
algorithm uses the division algorithm repeatedly to obtain 0 and b | a,
then gcd(a,b) = |b|. The next observation provides the basis for the Euclidean
algorithm. If a=bq+r, then (a,b)=(b,r). Thus given integers a>b>0, the Euclidean
algorithm uses the division algorithm repeatedly to obtain
a = bq1 + r1, with 0
 r1<
b r1<
b
b = r1q2 + r2, with 0
 r2<
r1, r2<
r1,
etc.
Since r1 > r2 > . . . , the remainders get smaller and
smaller, and after a finite number of steps we obtain a remainder rn+1
= 0. Thus gcd(a,b) = gcd(b,r1) = . . . = rn.
1.2.1. Definition. The nonzero integers a and b are said to be
relatively prime if (a,b)=1.
1.2.2 Proposition. Let a,b be nonzero integers. Then (a,b)=1 if and
only if there exist integers m,n such that
ma + nb = 1 .
1.2.3 Proposition. Let a,b,c be integers.
- (a) If b | ac, then b | (a,b)c.
- (b) If b | ac and (a,b)=1, then b | c.
- (c) If b | a, c | a and (b,c)=1, then bc | a.
- (d) (a,bc)=1 if and only if (a,b)=1 and (a,c)=1.
1.2.4. Definition. An integer p>1 is called a prime number if its
only divisors are � 1 and � p. An integer a > 1 is called
composite if it is not prime.
1.2.5. Lemma. [Euclid] An integer p>1 is prime if and only if it
satisfies the following property: If p | ab for integers a and b, then either p
| a or p | b.
1.2.6. Theorem. [Fundamental Theorem of Arithmetic] Any integer a>1
can be factored uniquely as a product of prime numbers, in the form
a = p1m1 p2m2
� � � pnmn
where p1 < p2 < � � � < pn and the exponents m1,
m2 , . . . , mn are all positive.
1.2.7. Theorem. [Euclid] There exist infinitely many prime numbers.
1.2.8. Definition. A positive integer m is called the least common
multiple of the nonzero integers a and b if
- (i) m is a multiple of both a and b, and
- (ii) any multiple of both a and b is also a multiple of m.
We will use the notation lcm[a,b] for the least common multiple of a and b.
1.2.9. Proposition. Let a and b be positive integers with prime
factorizations
a = p1a1 p2a2
� � � pnan and b = p1b1
p2b2 � � � pnbn
,
where ai
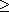 0 and bi 0 and bi
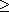 0 for all i
(allowing use of the same prime factors.) 0 for all i
(allowing use of the same prime factors.)
For each i let di =min { ai, bi } and let mi
=max { ai, bi }. Then we have the following
factorizations:
- (a) gcd(a,b) = p1d1 p2d2
� � � pndn
- (b) lcm[a,b] = p1m1 p2m2
� � � pnmn
Congruences
1.3.1. Definition. Let n be a positive integer. Integers a and b are said
to be congruent modulo n if they have the same remainder when divided by
n. This is denoted by writing a
 b (mod n). b (mod n).
1.3.2. Proposition. Let a,b, and n>0 be integers. Then a
 b (mod n)
if and only if n | (a-b). b (mod n)
if and only if n | (a-b).
When working with congruence modulo n, the integer n is called the
modulus. By the preceding proposition, a
 b (mod n)
if and only if a-b=nq for some integer q. We can write this in the form a=b+nq,
for some integer q. This observation gives a very useful method of replacing a
congruence with an equation (over Z). On the other hand, Proposition
1.3.3 shows that any equation can be converted to a congruence modulo n by
simply changing the = sign to b (mod n)
if and only if a-b=nq for some integer q. We can write this in the form a=b+nq,
for some integer q. This observation gives a very useful method of replacing a
congruence with an equation (over Z). On the other hand, Proposition
1.3.3 shows that any equation can be converted to a congruence modulo n by
simply changing the = sign to
 . In doing
so, any term congruent to 0 can simply be omitted. Thus the equation a=b+nq
would be converted back to a . In doing
so, any term congruent to 0 can simply be omitted. Thus the equation a=b+nq
would be converted back to a
 b (mod n). b (mod n).
1.3.3 Proposition. Let n>0 be an integer. Then the following
conditions hold for all integers a,b,c,d:
- (a) If a
 c (mod
n) and b c (mod
n) and b
 d (mod
n), then d (mod
n), then
then a
 b b
 c c
 d (mod
n), and ab d (mod
n), and ab
 cd
(mod n). cd
(mod n).
- (b) If a+c
 a+d
(mod n), then c a+d
(mod n), then c
 d (mod
n). d (mod
n).
If ac
 ad
(mod n) and (a,n)=1, then c ad
(mod n) and (a,n)=1, then c
 d (mod
n). d (mod
n).
1.3.4. Proposition. Let a and n>1 be integers. There exists an integer b
such that ab
 1 (mod n)
if and only if (a,n)=1. 1 (mod n)
if and only if (a,n)=1.
1.3.5. Theorem. The congruence ax
 b (mod n)
has a solution if and only if b is divisible by d, where d=(a,n). b (mod n)
has a solution if and only if b is divisible by d, where d=(a,n).
If d | b, then there are d distinct solutions modulo n, and these solutions are
congruent modulo n / d.
1.3.6. Theorem. [Chinese Remainder Theorem] Let n and m be positive
integers, with (n,m)=1. Then the system of congruences
x
 a (mod n)
x a (mod n)
x  b
(mod m) b
(mod m)
has a solution. Moreover, any two solutions are congruent modulo mn.
1.4.1. Definition. Let a and n>0 be integers. The set of all integers
which have the same remainder as a when divided by n is called the congruence
class of a modulo n, and is denoted by [a]n, where
[a]n = { x
 Z | x Z | x
 a (mod n)
}. a (mod n)
}.
The collection of all congruence classes modulo n is called the
set of integers modulo n, denoted by Zn.
1.4.2 Proposition. Let n be a positive integer, and let a,b be any
integers. Then the addition and multiplication of congruence classes given below
are well-defined:
[a]n + [b]n = [a+b]n ,
[a]n[b]n = [ab]n.
1.4.3. Definition. If [a]n belongs to Zn,
and [a]n[b]n = [0]n for some nonzero congruence
class [b]n, then [a]n is called a divisor of zero,
modulo n.
1.4.4. Definition. If [a]n belongs to Zn,
and [a]n[b]n = [1]n, for some congruence class
[b]n, then [b]n is called a multiplicative inverse
of [a]n and is denoted by [a]n-1.
In this case, we say that [a]n and [b]n are invertible
elements of Zn, or units of Zn.
1.4.5. Proposition. Let n be a positive integer.
- (a) The congruence class [a]n has a multiplicative
inverse in Zn if and only if (a,n)=1.
- (b) A nonzero element of Zn either has a
multiplicative inverse or is a divisor of zero.
1.4.6. Corollary. The following conditions on the modulus n > 0 are
equivalent:
- (1) The number n is prime.
- (2) Zn has no divisors of zero, except [0]n.
- (3) Every nonzero element of Zn has a
multiplicative inverse.
1.4.7. Definition. Let n be a positive integer. The number of positive
integers less than or equal to n which are relatively prime to n will be denoted
by 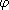 (n).
This function is called Euler's phi-function, or the totient function. (n).
This function is called Euler's phi-function, or the totient function.
1.4.8. Proposition. If the prime factorization of n is n = p1m1
p2m2 � � � pnmn
, then
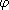 (n) =
n(1-1/p1)(1-1/p2) � � � (1-1/pk). (n) =
n(1-1/p1)(1-1/p2) � � � (1-1/pk).
1.4.9. Definition. The set of units of Zn, the
congruence classes [a]n, such that (a,n)=1, will be denoted by
Zn�.
The following theorem shows that raising any congruence class in Zn�
to the power
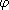 (n)
yields the congruence class of 1. It is possible to give a purely number
theoretic proof at this point, but in
Example 3.2.12
there is a more elegant proof using elementary group theory. (n)
yields the congruence class of 1. It is possible to give a purely number
theoretic proof at this point, but in
Example 3.2.12
there is a more elegant proof using elementary group theory.
1.4.11. Theorem. [Euler] If (a,n)=1, then a
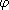 (n) (n)
 1 (mod n). 1 (mod n).
1.4.12 Corollary. [Fermat] If p is prime, then ap
 a (mod p),
for any integer a. a (mod p),
for any integer a.
|

