Localization in integral domains
5.8.9. Proposition. Let D be an integral domain with quotient field Q(D),
and let P be a prime ideal of D. Then
DP = { ab-1
 Q(D) | b Q(D) | b
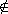 P } P }
is an integral domain with D
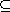 DP DP
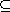 Q(D). Q(D).
5.8.10. Definition. Let D be an integral domain with quotient field
Q(D), and let P be a prime ideal of D. Then
DP = { ab-1
 Q(D) | b Q(D) | b
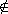 P } P }
is called the localization of D at P.
If I is any ideal of D, then
IP = { ab-1
 Q(D) | a Q(D) | a
 I and b I and b
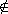 P } P }
is called the extension of I to DP.
5.8.11. Theorem. Let D be an integral domain with quotient field Q(D),
and let P be a prime ideal of D.
(a) If J is any proper ideal of DP, then there exists an ideal
I of D with I
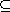 P such
that J = IP. If J is a prime ideal, then so is I. P such
that J = IP. If J is a prime ideal, then so is I.
(b) If J is any prime ideal of D with J
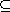 P, then
JP is a prime ideal of DP with D P, then
JP is a prime ideal of DP with D
 JP
= J. JP
= J.
(c) There is a one-to-one correspondence between prime ideals of DP
and prime ideals of D that are contained in P. Furthermore, PP is the
unique maximal ideal of DP.
Noncommutative examples
We want to include, among other examples, the study of n�n matrices. Recall that
if F is a field, then the set of n�n matrices Mn(F) corresponds to
the set of linear transformations of an n-dimensional vector space over F. This
is a special case of the most general example of a ring with identity. Just as
permutation groups are the generic groups (as shown by Cayley's theorem), the
generic examples of rings are found in studying endomorphisms of abelian groups.
Example. 5.5.1. (Endomorphisms of abelian groups)
Let A be an abelian group, with its operation denoted by +. Let R be the set of
all endomorphisms of A. That is, R is the set of all group homomorphisms f:A->A.
We can define addition and multiplication of elements of R as follows: if f,g
 R, then R, then
(f+g) (x) = f(x) + g(x) and (f . g) (x) = f(g(x))
for all x  A. A.
We need to repeat
Definition 5.1.1,
dropping the assumption that multiplication is commutative. We will, however,
assume that all rings have a multiplicative identity element. It can then be
shown that the set of all endomorphisms of an abelian group A, denoted by
End(A), forms a ring.
Definition A ring R is a set with two binary operations,
denoted by addition and multiplication, such that the following properties hold:
(i) For all a,b,c
 R, a+(b+c) =
(a+b)+c and a(bc) = (ab)c. R, a+(b+c) =
(a+b)+c and a(bc) = (ab)c.
(ii) For all a,b
 R, a+b = b+a. R, a+b = b+a.
(iii) For all a,b,c
 R, a(b+c) =
ab+ac and (a+b)c = ac+bc. R, a(b+c) =
ab+ac and (a+b)c = ac+bc.
(iv) The set R contains an additive identity element, denoted by
0, and a multiplictive identity element, denoted by 1, such that a+0 = a,
1a = a, and a1=a, for all a
 R. R.
(v) For each a
 R, the
equation a+x = 0 has a solution x = -a in R, the additive inverse of a. R, the
equation a+x = 0 has a solution x = -a in R, the additive inverse of a.
Example. 5.5.2. (Polynomial Rings)
Let R be any ring. We let R[x] denote the set of infinite tuples
(a0,a1,a2,...)
such that ai
 R for all i,
and ai R for all i,
and ai
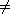 0 for only
finitely many terms ai. Two sequences are equal if and only if all
corresponding terms are equal. We introduce addition and multiplication as
follows: 0 for only
finitely many terms ai. Two sequences are equal if and only if all
corresponding terms are equal. We introduce addition and multiplication as
follows:
(a0,a1,a2,...) + (b0,b1,b2,...)
= (a0+b0,a1+b1,a2+b2,...)
(a0,a1,a2,...) . (b0,b1,b2,...)
= (c0,c1,c2,...),
where cn =
 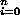 ai bn-i.
ai bn-i.
With these operations it can be shown that R[x] is a ring.
We can identify a
 R with
(a,0,0,...) R with
(a,0,0,...)  R[x], and so if R has an identity 1, then (1,0,0,...) is an identity for R[x].
If we let x=(0,1,0,...), then the elements of R[x] can be expressed in the form
R[x], and so if R has an identity 1, then (1,0,0,...) is an identity for R[x].
If we let x=(0,1,0,...), then the elements of R[x] can be expressed in the form
a0 + a1 x + . . . + am-1 xm-1 + am
xm,
allowing us to use our previous notation for the ring of polynomials over R
in the indeterminate x. Note that although the elements of R need not
commute with each other, they do commute with the indeterminate x.
If n is the largest nonnegative integer such that an
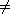 0, then we
say that the polynomial has degree n, and an is called the
leading coefficient of the polynomial. 0, then we
say that the polynomial has degree n, and an is called the
leading coefficient of the polynomial.
Example. 5.5.3. (Differential operator rings)
Consider the homogeneous linear differential equation
an(x) Dn y + . . . + a1(x) D y + a0(x)
y = 0,
where the solution y(x) is a polynomial with complex coefficients, and the terms
ai(x) also belong to C[x]. The equation can be
written in compact form as L(y)=0, where L is the differential operator
an(x) Dn + . . . + a1(x) D + a0(x),
with D = d/dx. Thus the differential operator can be thought of as a polynomial
in the two indeterminates x and D, but in this case the indeterminates do not
commute, since
D(x y(x)) = y(x) + x D(y(x)),
yielding the identity
Dx=1+xD.
Repeated use of this identity makes it possible to write the composition of two
differential operators in the standard form
a0(x) + a1(x) D + . . . + an(x) Dn,
and we denote the resulting ring by C[x][D].
Example. 5.5.4. (Group algebras)
Let K be a field, and let G be a finite group of order n, with elements 1=g1,
g2, . . . , gn. The group algebra KG is defined to
be the n-dimensional vector space over K with the elements of G as a basis.
Vector addition is used as the addition in the ring. Elements of KG can be
described as sums of the form

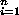 ci
gi ci
gi
and multiplication is defined as for polynomials, where the product gi
gj is given by the product in G.
Example. 5.5.5. (Matrix rings)
Let R be a ring. We let Mn(R) denote the set of all n�n matrices with
entries in R.
For [aij] and [bij] in Mn(R), we use
componentwise addition
[aij] + [bij] = [aij+bij]
and the multiplication is given by
[ajk] [bjk] = [cjk],
where [cij] is the matrix whose j,k-entry is
cjk =
 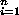 aji bik.
aji bik.
5.5.3. Definition. Let R be a ring with identity 1, and let a
 R. If ab=0
for some nonzero b R. If ab=0
for some nonzero b
 R, then a is
called a left zero divisor. Similarly, if ba=0 for some nonzero b R, then a is
called a left zero divisor. Similarly, if ba=0 for some nonzero b
 R, then a is
called a right zero divisor. If a is neither a left zero divisor nor a
right zero divisor, then a is called a regular element. R, then a is
called a right zero divisor. If a is neither a left zero divisor nor a
right zero divisor, then a is called a regular element.
The element a  R is said to be invertible if there exists an element b
R is said to be invertible if there exists an element b
 R such that
ab=1 and ba=1. The element a is also called a unit of R, and its
multiplicative inverse is usually denoted by a-1. R such that
ab=1 and ba=1. The element a is also called a unit of R, and its
multiplicative inverse is usually denoted by a-1.
The set of all units of R is denoted by R�.
5.5.4. Proposition. Let R be a ring. Then the set R� of
units of R is a group under the multiplication of R.
5.5.5. Definition. A ring R in which each nonzero element is a unit is
called a division ring or skew field.
Example. 5.5.8. (The quaternions)
The following subset of M2(C) is called the set of
quaternions, and provides the best known example of a division ring that is
not a field.
Q = a 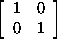 + b + b
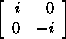 + c + c
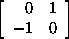 + d + d
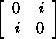
See Example
3.3.7 for the group of quaternion units.
Isomorphism theorems
5.6.1. Definition. Let R be a ring. A nonempty subset I of R is called a
left ideal of R if
(i) a  b
b  I for all
a,b I for all
a,b  I and
(ii) ra I and
(ii) ra  I
for all a I
for all a  I
and r I
and r  R. R.
The subset I is called a right ideal of R if
(i) a  b
b  I for all
a,b I for all
a,b  I and
(ii) ar I and
(ii) ar  I
for all a I
for all a  I
and r I
and r  R. R.
The subset I is called a two-sided ideal or simply an ideal of R
if it is both a left ideal and a right ideal.
For any ring R, it is clear that the set {0} is an ideal, which we will refer
to as the trivial ideal. Another ideal of R is the ring R itself.
5.6.2. Definition. Let R be a ring, and let a
 R. The left
ideal R. The left
ideal
Ra = { x  R |
x = ra for some r R |
x = ra for some r
 R } R }
is called the principal left ideal generated by a.
5.6.3. Proposition. Let R be a ring, and let I,J be left ideals of R.
The following subsets of R are left ideals.
(a) I  J;
J;
(b) I + J = { x
 R | x = a + b
for some a R | x = a + b
for some a  I,
b I,
b  J }; J };
(c) IJ = {
 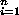 ai bi | ai
ai bi | ai
 I, bi I, bi
 J, n J, n
 Z+
}. Z+
}.
Example. 5.6.1. (Ideals of Mn(R))
Let R be a ring, and let Mn(R) be the ring of matrices over R. If I
is an ideal of R, then the set Mn(I) of all matrices with entries in
I is an ideal of S. Conversely, every ideal of S is of this type.
5.6.4. Theorem. If I is an ideal of the ring R, then R/I is a ring.
5.6.5. Definition. Let I be an ideal of the ring R. With the following
addition and multiplication for all a,b
 R, the set of
cosets R, the set of
cosets
{ a+I | a  R }
is denoted by R/I, and is called the factor ring of R modulo I. R }
is denoted by R/I, and is called the factor ring of R modulo I.
(a+I) + (b+I) = (a+b) + I and (a+I)(b+I) = ab + I
Let I be a proper ideal of the ring R. Then I is said to be a completely
prime ideal of R if for all a,b
 R it is true
that ab R it is true
that ab  I
implies a I
implies a  I
or b I
or b  I. I.
As in the commutative case, a ring is called a domain if (0) is a
completely prime ideal. An element c of R is said to be regular if xc = 0
or cx = 0 implies x = 0, for all x
 R. Thus a
ring is a domain if and only if every nonzero element is regular. R. Thus a
ring is a domain if and only if every nonzero element is regular.
5.7.1. Definition. Let R and S be rings. A function
 :R->S is
called a ring homomorphism if :R->S is
called a ring homomorphism if
(i)  (a+b)
= (a+b)
=  (a) + (a) +
 (b), for
all a,b (b), for
all a,b  R, R,
(ii)  (ab)
= (ab)
=  (a) (a)
 (b), for
all a,b (b), for
all a,b  R,
and R,
and
(iii)
 (1) = 1. (1) = 1.
A ring homomorphism that is one-to-one and onto is called an isomorphism.
If there is an isomorphism from R onto S, we say that R is isomorphic to
S, and write R
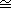 S. An
isomorphism from the ring R onto itself is called an automorphism of R. S. An
isomorphism from the ring R onto itself is called an automorphism of R.
5.7.2. Proposition. Any ring R is isomorphic to a subring of an
endomorphism ring End(A), for some abelian group A.
5.7.4. Definition. Let
 :R->S be a
ring homomorphism. The set :R->S be a
ring homomorphism. The set
{ a  R | R |
 (a) = 0 } (a) = 0 }
is called the kernel of
 , denoted
by ker( , denoted
by ker( ). ).
5.7.5. Proposition. Let
 :R->S be a
ring homomorphism. :R->S be a
ring homomorphism.
(a) If a,b
 ker( ker( )
and r )
and r  R, then
a+b, a-b, ra, and ar belong to ker( R, then
a+b, a-b, ra, and ar belong to ker( ). ).
(b) The homomorphism
 is an
isomorphism if and only if ker( is an
isomorphism if and only if ker( )={0}
and )={0}
and  (R)=S. (R)=S.
5.7.6. Proposition. Let R and S be rings, let
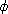 :R->S be a
ring homomorphism, and let :R->S be a
ring homomorphism, and let
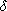 :{ x1,
x2, . . . , xn}->Z(S) be any mapping into the center of S.
Then there exists a unique ring homomorphism :{ x1,
x2, . . . , xn}->Z(S) be any mapping into the center of S.
Then there exists a unique ring homomorphism
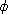 : R [ x1,
x2, . . . , xn] -> S such that : R [ x1,
x2, . . . , xn] -> S such that
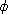 (r) = (r) =
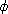 (r) for all
r (r) for all
r  R and R and
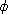 (xi)
= (xi)
= 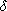 (xi),
for i=1,2,...,n. (xi),
for i=1,2,...,n.
Example. 5.7.2. Let G and H be finite groups, and let K be a field. If
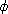 :G->H is a
group homomorphism, we can extend the mapping :G->H is a
group homomorphism, we can extend the mapping
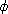 to a ring
homomorphism to a ring
homomorphism 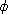 :KG->KH
as follows: :KG->KH
as follows:
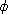 ( (
 x x
 G cx
x ) = G cx
x ) =  x x
 G cx G cx
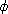 (x). (x).
5.7.7. Theorem. [Fundamental Homomorphism Theorem for Rings] Let
 :R->S be a
ring homomorphism. Then :R->S be a
ring homomorphism. Then
 (R) is a
subring of S, R/ker( (R) is a
subring of S, R/ker( )
is a ring, and )
is a ring, and
 (R) (R)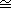 R/ker( R/ker( ). ).
5.7.8. Proposition. Let I be an ideal of the ring R.
(a) The natural projection mapping
 :R->R/I
defined by :R->R/I
defined by  (a)=a+I
for all a (a)=a+I
for all a  R
is a ring homomorphism, and ker( R
is a ring homomorphism, and ker( )
= I. )
= I.
(b) There is a one-to-one correspondence between the ideals of R/I and
ideals of R that contain I.
(c) If K is an ideal of R with I
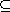 K K
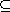 R, then
(R/I)/(K/I) R, then
(R/I)/(K/I)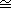 R/K. R/K.
5.7.9. Theorem. [Chinese Remainder Theorem] Let R be a ring, and let I1,
I2 be ideals of R such I1+I2=R. Then
( R / I1)
 ( R / I2) ( R / I2)
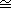 R / (I1 R / (I1
 I2). I2).
|

