Nilpotent groups
We now define and study a class of solvable groups that includes all finite
abelian groups and all finite p-groups.
7.8.1 Definition. For a group G we define the ascending central
series
Z1(G)
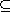 Z2(G) Z2(G)
 . . .
of G as follows: . . .
of G as follows:
Z1(G) is the center Z(G) of G;
Z2(G) is the unique subgroup of G with
Z1(G)
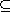 Z2(G)
and Z2(G) / Z1(G) = Z(G/Z1(G)). Z2(G)
and Z2(G) / Z1(G) = Z(G/Z1(G)).
We define Zi(G) inductively, in the same way.
The group G is called nilpotent if there exists a positive integer n with
Zn(G)=G.
7.8.2 Proposition. If G1, G2, . . . , Gn
are nilpotent groups, then so is
G = G1 � G2 � . . . � Gn.
7.8.3 Lemma. If P is a Sylow p-subgroup of a finite group G, then the
normalizer N(P) is equal to its own normalizer in G.
7.8.4 Theorem. The following conditions are equivalent for any finite
group G.
(1) G is nilpotent;
(2) no proper subgroup H of G is equal to its normalizer N(H);
(3) every Sylow subgroup of G is normal;
(4) G is a direct product of its Sylow subgroups.
7.8.5 Corollary. Let G be a finite nilpotent group of order n. If m is
any divisor of n, then G has a subgroup of order m.
7.8.6 Lemma. [Frattini's Argument] Let G be a finite group, and let H
be a normal subgroup of G. If P is any Sylow subgroup of H, then G=HN(P), and [G:H]
is a divisor of |N(P)|.
7.8.7 Proposition. A finite group is nilpotent if and only if every
maximal subgroup is normal.
Semidirect products
7.9.1 Definition. Let G be a group with subgroups N and K such that
(i) N is normal in G;
(ii) N  K = {e}; and
K = {e}; and
(iii) NK = G.
Then G is called the semidirect product of N by K.
Example. 7.9.6. (Dn is a semidirect product.)
Consider the dihedral group Dn, described by generators a of order n
and b of order 2, with the relation ba=a-1b. Then <a> is a normal
subgroup, <a> <b>={e},
and <a><b>=Dn. Thus the dihedral group is a semidirect product of a
cyclic subgroups of order n by a cyclic subgroup of order 2. <b>={e},
and <a><b>=Dn. Thus the dihedral group is a semidirect product of a
cyclic subgroups of order n by a cyclic subgroup of order 2.
Definition 7.9.1 describes an ``internal'' semidirect product. We now use the
automorphism group to give a general definition of an ``external'' semidirect
product.
7.9.2 Definition. Let G be a multiplicative group, and let X be an
abelian group, denoted additively. Let
 :G->Aut(X)
be a group homomorphism. The semidirect product of X and G relative to :G->Aut(X)
be a group homomorphism. The semidirect product of X and G relative to
 is is
X 
 G =
{ (x,a) | x G =
{ (x,a) | x  X, a
X, a  G } G }
with the operation (x1, a1) (x2, a2)
= ( x1 +
 (a1)
[x2], a1 a2), for x1, x2 (a1)
[x2], a1 a2), for x1, x2
 X and a1,
a2 X and a1,
a2  G. G.
7.9.3 Proposition. Let G be a multiplicative group, let X be an
additive group, and let
 :G->Aut(X)
be a group homomorphism. :G->Aut(X)
be a group homomorphism.
(a) The semidirect product X

 G is
a group. G is
a group.
(b) The set { (x,a)
 X X

 G |
x = 0 } is a subgroup of X G |
x = 0 } is a subgroup of X

 G
that is isomorphic to G. G
that is isomorphic to G.
(c) The set N = { (x,a)
 X X

 G |
a = e } is a normal subgroup of X G |
a = e } is a normal subgroup of X
 G
that is isomorphic to X, and (X G
that is isomorphic to X, and (X
 G)/N
is isomorphic to G. G)/N
is isomorphic to G.
We can now give a more general definition. We say that Zn

 Znx is the holomorph of Zn,
denoted by Hn.
Znx is the holomorph of Zn,
denoted by Hn.
7.9.4 Definition. Let G be a group and let X be an abelian group. If G
acts on X and a(x+y)=ax+ay, for all a G
and x,y G
and x,y X, then
we say that G acts linearly on X. X, then
we say that G acts linearly on X.
7.9.5 Proposition. Let G be a group and let X be an abelian group.
Then any group homomorphism from G into the group Aut(X) of all automorphisms of
X defines a linear action of G on X. Conversely, every linear action of G on X
arises in this way.
7.9.6 Proposition. Let G be a multiplicative group with a normal
subgroup N, and assume that N is abelian. Let
 :G->G/N be the
natural projection. The following conditions are equivalent: :G->G/N be the
natural projection. The following conditions are equivalent:
(1) There exists a subgroup K of G such that N K={e}
and NK=G; K={e}
and NK=G;
(2) There exists a homomorphism
 :G/N->G
such that :G/N->G
such that   is the identity on G/N;
is the identity on G/N;
(3) There exists a homomorphism
 :G/N->Aut(N)
such that N :G/N->Aut(N)
such that N

 (G/N)
(G/N)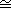 G. G.
Classification of groups of small order
In this section we study finite groups of a manageable size. Our first goal is
to classify all groups of order less than 16 (at which point the classification
becomes more difficult). Of course, any group of prime order is cyclic, and
simple abelian. A group of order 4 is either cyclic, or else each nontrivial
element has order 2, which characterizes the Klein four-group.
7.10.1 Proposition. Any nonabelian group of order 6 is isomorphic to S3.
7.10.2 Proposition. Any nonabelian group of order 8 is isomorphic
either to D4 or to the quaternion group Q.
7.10.3 Proposition. Let G be a finite group.
(a) Let N be a normal subgroup of G. If there exists a subgroup H such
that H N={e}
and |H|=[G:N], then G N={e}
and |H|=[G:N], then G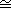 N N H.
H.
(b) Let G be a group with |G|=pnqm, for primes p,q.
If G has a unique Sylow p-subgroup P, and Q is any Sylow q-subgroup of G, then G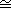 P P Q. Furthermore, if Q' is any other Sylow q-subgroup, then P
Q. Furthermore, if Q' is any other Sylow q-subgroup, then P Q' is isomorphic to P
Q' is isomorphic to P Q.
Q.
(c) Let G be a group with |G|=p2q, for primes p,q. Then G is
isomorphic to a semidirect product of its Sylow subgroups.
7.10.4 Lemma. Let G,X be groups, let
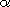 , ,
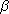 :G->Aut(X),
and let :G->Aut(X),
and let  , ,
 be the
corresponding linear actions of G on X. be the
corresponding linear actions of G on X.
Then X 
 G
G 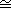 X X

 G if
there exists G if
there exists
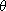
 Aut(G) such
that Aut(G) such
that 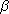 = =
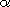 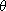 . .
7.10.5 Proposition. Any nonabelian group of order 12 is isomorphic to
one of
A4, D6, or Z3
 Z4. Z4.
The following table summarizes the above information on the isomorphism
classes of groups of order less than sixteen.
Order 2: Z2
Order 3: Z3
Order 4: Z4, Z2 � Z2
Order 5: Z5
Order 6: Z6, S3
Order 7: Z7
Order 8: Z8, Z4 � Z2,
Z2 � Z2 � Z2,
D4, Q
Order 9: Z9, Z3 � Z3
Order 10: Z10, D5
Order 11: Z11
Order 12: Z12, Z6 �
Z2 A4, D6, Z3
 Z4 Z4
Order 13: Z13
Order 14: Z14, D7
Order 15: Z15
7.10.6 Proposition. Let G be a finite simple group of order n, and let
H be any proper, nontrivial subgroup of G.
(a) If k = [G:H], then n is a divisor of k!.
(b) If H has m conjugates, then n is a divisor of m!.
7.10.7 Proposition. The alternating group A5 is the
smallest nonabelian simple group.
|

