Roots; unique factorization
4.1.1. Definition. Let F be a set on which two binary operations are
defined, called addition and multiplication, and denoted by + and �
respectively. Then F is called a field with respect to these operations
if the following properties hold:
- (i) Closure: For all a,b
 F the sum
a + b and the product a�b are uniquely defined and belong to F. F the sum
a + b and the product a�b are uniquely defined and belong to F.
- (ii) Associative laws: For all a,b,c
 F, F,
a+(b+c) = (a+b)+c and a�(b�c) = (a�b)�c.
- (iii) Commutative laws: For all a,b
 F, F,
a+b = b+a and a�b = b�a.
- (iv) Distributive laws: For all a,b,c
 F, F,
a�(b+c) = (a�b) + (a�c) and (a+b)�c
= (a�c) + (b�c).
- (v) Identity elements: The set F contains an additive
identity element, denoted by 0, such that for all a
 F, F,
a+0 = a and 0+a = a.
The set F also contains a multiplicative identity element, denoted by
1 (and assumed to be different from 0) such that for all a
 F, F,
a�1 = a and 1�a = a.
- (vi) Inverse elements: For each a
 F, the
equations F, the
equations
a+x = 0 and x+a = 0
have a solution x
 F, called
an additive inverse of a, and denoted by -a. F, called
an additive inverse of a, and denoted by -a.
For each nonzero element a
 F, the
equations F, the
equations
a�x = 1 and x�a = 1
have a solution x
 F, called
a multiplicative inverse of a, and denoted by a-1. F, called
a multiplicative inverse of a, and denoted by a-1.
4.1.4. Definition. Let F be a field. If am, am-1 ,
. . . , a1, a0
 F, then any
expression of the form F, then any
expression of the form
amxm + am-1xm-1 +
� � � + a1x + a0
is called a polynomial over F in the indeterminate x with
coefficients am, am-1, . . . , a0. The set of
all polynomials with coefficients in F is denoted by F[x].
If n is the largest nonnegative integer such that an
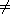 0, then we
say that the polynomial 0, then we
say that the polynomial
f(x) = anxn + � � � + a0
has degree n, written deg(f(x)) = n, and an is called the
leading coefficient of f(x).
If the leading coefficient is 1, then f(x) is said to be monic.
Two polynomials are equal by definition if they have the same degree and all
corresponding coefficients are equal. It is important to distinguish between the
polynomial f(x) as an element of F[x] and the corresponding polynomial
function from F into F defined by substituting elements of F in place of x.
If f(x) = amxm + � � � + a0 and c
 F, then f(c) =
amcm + � � � + a0. In fact, if F is a finite
field, it is possible to have two different polynomials that define the same
polynomial function. For example, let F be the field Z5
and consider the polynomials x5 -2x + 1 and 4x + 1. For any c F, then f(c) =
amcm + � � � + a0. In fact, if F is a finite
field, it is possible to have two different polynomials that define the same
polynomial function. For example, let F be the field Z5
and consider the polynomials x5 -2x + 1 and 4x + 1. For any c
 Z5,
by Fermat's
theorem we have c5 Z5,
by Fermat's
theorem we have c5
 c (mod 5),
and so c (mod 5),
and so
c5 -2c + 1
 -c + 1 -c + 1
 4c + 1
(mod 5), 4c + 1
(mod 5),
which shows that x5 -2x + 1 and 4x + 1 are identical, as functions.
For the polynomials
f(x) = amxm + am-1xm-1
+ � � � + a1x + a0
and
g(x) = bnxn + bn-1xn-1
+ � � � + b1x + b0,
the sum of f(x) and g(x) is defined by just adding corresponding coefficients.
The product f(x)g(x) is defined to be
ambnxn+m + � � � + (a2b0
+ a1b1 + a0b2)x2 + (a1b0
+ a0b1)x + a0b0.
The coefficient ck of xk in f(x)g(x) can be described by
the formula
ck =

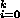 ai
bk-i. ai
bk-i.
This definition of the product is consistent with what we would expect to obtain
using a naive approach: Expand the product using the distributive law repeatedly
(this amounts to multiplying each term be every other) and then collect similar
terms.
4.1.5. Proposition. If f(x) and g(x) are nonzero polynomials in F[x],
then f(x)g(x) is nonzero and
deg(f(x)g(x)) = deg(f(x)) + deg(g(x)).
4.1.6. Corollary. If f(x),g(x),h(x)
 F[x], and
f(x) is not the zero polynomial, then F[x], and
f(x) is not the zero polynomial, then
f(x)g(x) = f(x)h(x) implies g(x) = h(x).
4.1.7. Definition. Let f(x),g(x)
 F[x]. If f(x)
= q(x)g(x) for some q(x) F[x]. If f(x)
= q(x)g(x) for some q(x)
 F[x], then we
say that g(x) is a factor or divisor of f(x), and we write g(x) |
f(x). F[x], then we
say that g(x) is a factor or divisor of f(x), and we write g(x) |
f(x).
The set of all polynomials divisible by g(x) will be denoted by < g(x) >.
4.1.8. Lemma. For any element c
 F, and any
positive integer k, F, and any
positive integer k,
(x - c) | (xk - ck).
4.1.9. Theorem. [Remainder Theorem] Let f(x)
 F[x] be a
nonzero polynomial, and let c F[x] be a
nonzero polynomial, and let c
 F. Then there
exists a polynomial q(x) F. Then there
exists a polynomial q(x)
 F[x] such
that F[x] such
that
f(x) = q(x)(x - c) + f(c).
Moreover, if f(x) = q1(x)(x - c) + k, where q1(x)
 F[x] and k F[x] and k
 F, then q1(x)
= q(x) and k = f(c). F, then q1(x)
= q(x) and k = f(c).
4.1.10. Definition. Let f(x) = amxm + � � � + a0
 F[x]. An
element c F[x]. An
element c  F
is called a root of the polynomial f(x) if f(c) = 0, that is, if c is a
solution of the polynomial equation f(x) = 0 . F
is called a root of the polynomial f(x) if f(c) = 0, that is, if c is a
solution of the polynomial equation f(x) = 0 .
4.1.11. Corollary. Let f(x)
 F[x] be a
nonzero polynomial, and let c F[x] be a
nonzero polynomial, and let c
 F. Then c is
a root of f(x) if and only if x-c is a factor of f(x). That is, F. Then c is
a root of f(x) if and only if x-c is a factor of f(x). That is,
f(c) = 0 if and only if (x-c) | f(x).
4.1.12 Corollary. A polynomial of degree n with coefficients in the field
F has at most n distinct roots in F.
4.2.1. Theorem. [Division Algorithm] For any polynomials f(x) and g(x)
in F[x], with g(x)
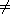 0, there
exist unique polynomials q(x),r(x) 0, there
exist unique polynomials q(x),r(x)
 F[x] such
that F[x] such
that
f(x) = q(x)g(x) + r(x),
where either deg(r(x)) < deg(g(x)) or r(x) = 0.
4.2.2. Theorem Let I be a subset of F[x] that satisfies the following
conditions:
- (i) I contains a nonzero polynomial;
- (ii) if f(x),g(x)
 I, then
f(x)+g(x) I, then
f(x)+g(x)  I;
I;
- (iii) if f(x)
 I and
q(x) I and
q(x)  F[x], then q(x)f(x)
F[x], then q(x)f(x)
 I. I.
If d(x) is any nonzero polynomial in I of minimal degree, then
I = { f(x)
 F[x] |
f(x)=q(x)d(x) for some q(x) F[x] |
f(x)=q(x)d(x) for some q(x)
 F[x] }. F[x] }.
4.2.3. Definition. A monic polynomial d(x)
 F[x] is
called the greatest common divisor of f(x),g(x) F[x] is
called the greatest common divisor of f(x),g(x)
 F[x] if F[x] if
- (i) d(x) | f(x) and d(x) | g(x) , and
- (ii) if h(x) | f(x) and h(x) | g(x) for some h(x)
 F[x],
then h(x) | d(x). F[x],
then h(x) | d(x).
The greatest common divisor of f(x) and g(x) is denoted by gcd(f(x),g(x)).
If gcd(f(x),g(x)) = 1, then the polynomials f(x) and g(x) are said to be
relatively prime.
4.2.4. Theorem. For any nonzero polynomials f(x),g(x)
 F[x] the
greatest common divisor gcd(f(x),g(x)) exists and can be expressed as a linear
combination of f(x) and g(x), in the form F[x] the
greatest common divisor gcd(f(x),g(x)) exists and can be expressed as a linear
combination of f(x) and g(x), in the form
gcd(f(x),g(x)) = a(x)f(x) + b(x)g(x)
for some a(x),b(x)
 F[x]. F[x].
Example. 4.2.3. (Euclidean algorithm for polynomials) Let f(x),g(x)
 F[x] be
nonzero polynomials. We can use the division algorithm to write F[x] be
nonzero polynomials. We can use the division algorithm to write
f(x) = q(x)g(x) + r(x),
with deg(r(x))<deg(g(x)) or r(x) = 0.
- If r(x) = 0, then g(x) is a divisor of f(x), and so gcd(f(x),g(x)) =
cg(x), for some c
 F. F.
- If r(x)
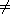 0, then
it is easy to check that gcd(f(x),g(x)) = gcd(g(x),r(x)). 0, then
it is easy to check that gcd(f(x),g(x)) = gcd(g(x),r(x)).
This step reduces the degrees of the polynomials involved, and so repeating the
procedure leads to the greatest common divisor of the two polynomials in a
finite number of steps.
The Euclidean algorithm for polynomials is similar to the Euclidean algorithm
for finding the greatest common divisor of nonzero integers. The polynomials
a(x) and b(x) for which
gcd(f(x),g(x)) = a(x)f(x) + b(x)g(x)
can be found just as for integers (see the
Euclidean
algorithm for integers).
4.2.5. Proposition. Let p(x),f(x),g(x)
 F[x]. If
gcd(p(x),f(x)) = 1 and p(x) | f(x)g(x), then p(x) | g(x). F[x]. If
gcd(p(x),f(x)) = 1 and p(x) | f(x)g(x), then p(x) | g(x).
4.2.6. Definition. A nonconstant polynomial (that is, a polynomial
with positive degree) is said to be irreducible over the field F if it
cannot be factored in F[x] into a product of polynomials of lower degree. It is
said to be reducible over F if such a factorization exists.
4.2.7. Proposition. A polynomial of degree 2 or 3 is irreducible over
the field F if and only if it has no roots in F.
4.2.8 Lemma. The nonconstant polynomial p(x)
 F[x] is
irreducible over F if and only if for all f(x),g(x) F[x] is
irreducible over F if and only if for all f(x),g(x)
 F[x], F[x],
p(x) | (f(x)g(x)) implies p(x) | f(x) or p(x) | g(x).
4.2.9. Theorem. [Unique Factorization] Any nonconstant polynomial with
coefficients in the field F can be expressed as an element of F times a product
of monic polynomials, each of which is irreducible over the field F . This
expression is unique except for the order in which the factors occur.
4.2.10. Definition. Let f(x)
 F[x]. An
element c F[x]. An
element c  F
is said to be a root of multiplicity n F
is said to be a root of multiplicity n
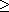 1 of f(x) if 1 of f(x) if
(x - c)n | f(x) but (x - c)n+1
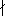 f(x). f(x).
4.2.11. Proposition. A nonconstant polynomial f(x) over the field
R of real numbers has no repeated factors if and only if
gcd(f(x),f'(x))=1, where f'(x) is the derivative of f(x).
Example. 4.2.4. (Partial fractions) Let f(x)/g(x) be a rational
function. The first step in achieving a partial fraction decomposition of
f(x)/g(x) is to use
Theorem
4.2.9 to write g(x) as a product of irreducible polynomials.
If g(x)=p(x)q(x), where p(x) and q(x) are relatively prime, then by
Theorem
4.2.4 there exist polynomials a(x) and b(x) with
a(x)p(x)+b(x)q(x)=1.
Dividing by p(x)q(x) allows us to write
1 / p(x)q(x) = a(x)/q(x) + b(x)/p(x),
and so
f(x) / g(x) = (f(x)a(x)) / q(x) + (f(x)b(x)) / p(x).
This process can be extended by induction until f(x)/g(x) is written as a sum of
rational functions, where in each case the denominator is a power of an
irreducible polynomial.
The next step in the partial fraction decomposition is to expand the terms of
the form h(x)/p(x)n. Using the division algorithm, we can write
h(x) / p(x)n = a(x) + r(x)/p(x)n,
where deg(r(x)) < deg(p(x)n). Then we can divide r(x) by p(x)n-1
to obtain
r(x) = b(x)p(x)n-1 + c(x),
where deg(c(x)) < deg(p(x)n-1). This gives us
r(x) / p(x)n = b(x)/p(x) + c(x)/p(x)n,
in which deg(b(x)) < deg(p(x)). This can be continued by induction, to obtain
h(x) / p(x)n= a(x) + b(x)/p(x) + � � � + t(x)/p(x)n,
in which the numerators b(x),...,t(x) all have lower degree than that of p(x).
Construction of extension fields
4.4.1. Definition. Let E and F be fields. If F is a subset of E and has
the operations of addition and multiplication induced by E, then F is called a
subfield of E, and E is called an extension field of F.
4.4.2. Definition. Let F be a field, and let p(x) be a fixed
polynomial over F. If a(x),b(x)
 F[x], then we
say that a(x) and b(x) are congruent modulo p(x), written F[x], then we
say that a(x) and b(x) are congruent modulo p(x), written
a(x)
 b(x) (mod
p(x)), b(x) (mod
p(x)),
if p(x) | (a(x)-b(x)). The set
{ b(x)
 F[x] | a(x) F[x] | a(x)
 b(x) (mod
p(x)) } b(x) (mod
p(x)) }
is called the congruence class of a(x), and will be denoted by [a(x)].
The set of all congruence classes modulo p(x) will be denoted by
F[x]/<p(x)>.
4.4.3. Proposition. Let F be a field, and let p(x) be a nonzero
polynomial in F[x]. For any a(x)
 F[x], the
congruence class [a(x)] modulo p(x) contains a unique representative r(x) with
deg(r(x))<deg(p(x)) or r(x)=0. F[x], the
congruence class [a(x)] modulo p(x) contains a unique representative r(x) with
deg(r(x))<deg(p(x)) or r(x)=0.
4.4.4. Proposition. Let F be a field, and let p(x) be a nonzero
polynomial in F[x]. For any polynomials a(x),b(x),c(x), and d(x) in F[x], the
following conditions hold:
- (a) If a(x)
 c(x)
(mod p(x)) and b(x) c(x)
(mod p(x)) and b(x)
 d(x)
(mod p(x)), then d(x)
(mod p(x)), then
a(x)+b(x)
 c(x)+d(x) (mod p(x))
c(x)+d(x) (mod p(x))
and
a(x)b(x)
 c(x)d(x) (mod p(x)).
c(x)d(x) (mod p(x)).
- (b) If gcd(a(x),p(x))=1, then
a(x)b(x)
 a(x)c(x) (mod p(x))
a(x)c(x) (mod p(x))
implies
b(x)
 c(x)
(mod p(x)). c(x)
(mod p(x)).
4.4.5. Proposition. Let F be a field, and let p(x) be a nonzero
polynomial in F[x]. For any a(x)
 F[x], the
congruence class [a(x)] has a multiplicative inverse in F[x]/<p(x)> if and only
if gcd(a(x),p(x))=1. F[x], the
congruence class [a(x)] has a multiplicative inverse in F[x]/<p(x)> if and only
if gcd(a(x),p(x))=1.
4.4.6. Theorem. Let F be a field, and let p(x) be a nonconstant
polynomial over F. Then F[x]/<p(x)> is a field if and only if p(x) is
irreducible over F.
4.4.7. Definition. Let F1 and F2 be fields. A
function  :
F1 -> F2 is called an isomorphism of fields if :
F1 -> F2 is called an isomorphism of fields if
- (i)
 is
one-to-one and onto, is
one-to-one and onto,
- (ii)
 (a+b) = (a+b) =
 (a) + (a) +
 (b),
for all a,b (b),
for all a,b
 F1,
and F1,
and
- (iii)
 (ab) = (ab) =
 (a) (a)
 (b) for
all a,b (b) for
all a,b  F1. F1.
4.4.8 Theorem. [Kronecker] Let F be a field, and let f(x) be any
nonconstant polynomial in F[x]. Then there exists an extension field E of F and
an element u  E such that f(u)=0.
E such that f(u)=0.
4.4.9 Corollary. Let F be a field, and let f(x) be any nonconstant
polynomial in F[x]. Then there exists an extension field E of F over which f(x)
can be factored into a product of linear factors.
Polynomials over Q, R, and C
4.3.1. Proposition. Let f(x) = anxn + an-1xn-1
+ � � � + a1x + a0 be a polynomial with integer
coefficients. If r/s is a rational root of f(x), with (r,s)=1, then r | a0
and s | an.
4.3.2. Definition. A polynomial with integer coefficients is called
primitive if the greatest common divisor of all of its coefficients is 1.
4.3.3 Lemma. Let p be a prime number, and let f(x) = g(x)h(x), where
- f(x) = amxm + � � � + a1x + a0,
- g(x) = bnxn + � � � + b1x + b0,
and
- and h(x) = ckxk + � � � + c1x + c0.
If bs and ct are the coefficients of g(x) and h(x) of
least index not divisible by p, then as+t is the coefficient of f(x)
of least index not divisible by p.
4.3.4. Theorem. [Gauss's Lemma] The product of two primitive
polynomials is itself primitive.
4.3.5. Theorem. A polynomial with integer coefficients that can be
factored into polynomials with rational coefficients can also be factored into
polynomials of the same degree with integer coefficients.
4.3.6. Theorem. [Eisenstein's Irreducibility Criterion] Let
f(x) = anxn + an-1xn-1
+ � � � + a0
be a polynomial with integer coefficients. If there exists a prime number p such
that
an-1
 an-2 an-2
 . . . . . .
 a0 a0
 0 (mod p)
but 0 (mod p)
but
an
 0 (mod p) and a0
0 (mod p) and a0
 0 (mod p2),
0 (mod p2),
then f(x) is irreducible over the field of rational numbers.
4.3.7 Corollary. If p is prime, then the polynomial
 (x) = xp-1
+ � � � + x + 1 (x) = xp-1
+ � � � + x + 1
is irreducible over the field of rational numbers.
A.5.2 Theorem. [DeMoivre] For any positive integer n,
( cos + i sin
+ i sin )n
= cos(n )n
= cos(n ) +
i sin(n ) +
i sin(n ). ).
A.5.3. Corollary. For any positive integer n, the equation zn
= 1 has n distinct roots in the set of complex numbers.
Definition. The roots in C of the polynomial xn-1
are called the complex nth roots of unity.
A complex nth root of unity is said to be primitive if it is a
root of the polynomial xn-1, but is not a root of xm-1 for
any positive integer m<n.
Example. A.5.3. If zn = u, then (z )n
= u, where )n
= u, where  is any nth root of unity. Thus if all nth roots of unity are
already known, it is easy to find the nth roots of any complex number.
In general, the nth roots of r(cos
is any nth root of unity. Thus if all nth roots of unity are
already known, it is easy to find the nth roots of any complex number.
In general, the nth roots of r(cos + i sin
+ i sin )
are )
are
r1/n (cos (( +
2k +
2k )/n) + i sin
(( )/n) + i sin
(( + 2k + 2k )/n)), )/n)),
for 1  k k
 n. n.
A.5.4. Theorem. [Fundamental Theorem of Algebra] Any polynomial of
positive degree with complex coefficients has a complex root.
A.5.5. Corollary. Any polynomial f(z) of degree n > 0 with complex
coefficients can be expressed as a product of linear factors, in the form
f(z) = c (z-z1) (z-z2) � � � (z-zn).
If z = a+bi is a complex number, then its complex conjugate, denoted by
z*, is z* = a-bi. Note that zz* = a2 + b2 and z+z* = 2a
are real numbers, whereas z-z* = (2b)i is a purely imaginary number.
Furthermore, z = z* if and only if z is a real number ( i.e., b = 0). It can be
checked that (z+w)* = z*+w* and (zw)* = z*w*.
A.5.6. Proposition. Let f(x) be a polynomial with real coefficients.
Then a complex number z is a root of f(x) if and only if z* is a root of f(x).
A.5.7. Theorem. Any polynomial with real coefficients can be factored
into a product of linear and quadratic terms with real coefficients.
A.5.8. Corollary. Any polynomial of odd degree that has real
coefficients must have a real root.
|

