Definition of a module
10.1.1 Definition. Let R be a ring, and let M be an abelian group. Then M
is called a left R-module if there exists a scalar multiplication
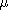 : R � M -> M
denoted by : R � M -> M
denoted by 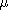 (r,m)=rm,
for all r (r,m)=rm,
for all r R and
all m R and
all m  M, M,
such that for all r,r1, r2
 R and all m,
m1, m2 R and all m,
m1, m2
 M, M,
(i) r(m1 + m2) = r m1 + r m2
(ii) ( r1 + r2 ) m = r1 m + r2 m
(iii) r1 ( r2 m ) = ( r1 r2 ) m
(iv) 1 m = m .
Example. 10.1.1. (Vector spaces over F are F-modules) If V is a vector
space over a field F, then it is an abelian group under addition of vectors. The
familiar rules for scalar multiplication are precisely those needed to show that
V is a module over the ring F.
Example. 10.1.2. (Abelian groups are Z-modules) If A
is an abelian group with its operation denoted additively, then for any element
x Z and any
positive integer n, we have defined nx to be the sum of x with itself n times.
This is extended to negative integers by taking sums of -x. With this familiar
multiplication, it is easy to check that A becomes a Z-module. Z and any
positive integer n, we have defined nx to be the sum of x with itself n times.
This is extended to negative integers by taking sums of -x. With this familiar
multiplication, it is easy to check that A becomes a Z-module.
Another way to show that A is a Z-module is to define a ring
homomorphism 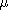 :Z->End(A)
by letting :Z->End(A)
by letting 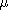 (n)=n1,
for all n (n)=n1,
for all n Z.
This is the familiar mapping that is used to determine the characteristic of the
ring End(A). The action of Z on A determined by this mapping is
the same one used in the previous paragraph. Z.
This is the familiar mapping that is used to determine the characteristic of the
ring End(A). The action of Z on A determined by this mapping is
the same one used in the previous paragraph.
If M is a left R-module, then there is an obvious definition of a
submodule of M: any subset of M that is a left R-module under the operations
induced from M. The subset {0} is called the trivial submodule, and is
denoted by (0). The module M is a submodule of itself, an improper
submodule. It can be shown that if M is a left R-module, then a subset N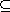 M
is a submodule if and only if it is nonempty, closed under sums, and closed
under multiplication by elements of R. M
is a submodule if and only if it is nonempty, closed under sums, and closed
under multiplication by elements of R.
If N is a submodule of RM, then we can form the factor group M/N.
There is a natural multiplication defined on the cosets of N: for any r R
and any x R
and any x M,
let r(x+N)=rx+N. If x+N=y+N, then x-y M,
let r(x+N)=rx+N. If x+N=y+N, then x-y N,
and so rx-ry=r(x-y) N,
and so rx-ry=r(x-y) N,
and this shows that scalar multiplication is well-defined. It follows that M/N
is a left R-module. N,
and this shows that scalar multiplication is well-defined. It follows that M/N
is a left R-module.
Any submodule of RR is called a left ideal of R. A
submodule of RR is called a right ideal of R, and it is clear
that a subset of R is an ideal if and only if it is both a left ideal and a
right ideal of R.
For any element m of the module M, we can construct the submodule
Rm = { x
 M | x = rm
for some r M | x = rm
for some r  R
}. R
}.
This is the smallest submodule of M that contains m, so it is called the
cyclic submodule generated by m. More generally, if X is any subset of M,
then the intersection of all submodules of M which contain X is the smallest
submodule of M which contains X. We will use the notation <X> for this
submodule, and call it the submodule generated by X. We must have Rx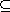 <X>
for all x <X>
for all x X,
and then it is not difficult to show that X,
and then it is not difficult to show that
< X > =
 x x XRx. XRx.
10.1.2 Definition. The left R-module M is said to be finitely
generated if there exist m1, m2, . . . , mn M
such that M
such that
M= 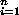 Rmi. Rmi.
In this case, we say that { m1, m2, . . . , mn
} is a set of generators for M. The module M is called cyclic if
there exists m M
such that M=Rm. M
such that M=Rm.
The module M is called a free module if there exists a subset X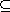 M
such that each element m M
such that each element m M
can be expressed uniquely as a finite sum M
can be expressed uniquely as a finite sum
m= 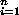 ai xi, with a1, . . . , an
ai xi, with a1, . . . , an R
and x1, . . . , xn R
and x1, . . . , xn X. X.
We note that if N is a submodule of M such that N and M/N are finitely
generated, then M is finitely generated. In fact, if x1, x2,
. . . , xn generate N and y1+N, y2+N, . . . , ym+N
generate M/N, then x1, . . . , xn, y1, . . . ,
ym generate M.
The module RR is the prototype of a free module, with generating
set {1}. If RM is a module, and X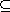 M,
we say that the set X is linearly independent if M,
we say that the set X is linearly independent if
 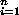 ai xi=0 implies ai=0 for i=1,...,n, for any
distinct x1, x2, . . . , xn
ai xi=0 implies ai=0 for i=1,...,n, for any
distinct x1, x2, . . . , xn
 X and any a1,
a2, . . . , an X and any a1,
a2, . . . , an
 R. Then a
linearly independent generating set for M is called a basis for M, and so
M is a free module if and only if it has a basis. R. Then a
linearly independent generating set for M is called a basis for M, and so
M is a free module if and only if it has a basis.
10.1.3 Definition. Let M and N be left R-modules. A function f:M -> N
is called an R-homomorphism if
f(m1 + m2) = f(m1) + f(m2)
and f(rm) = rf(m)
for all r R and
all m, m1, m2 R and
all m, m1, m2 M.
The set of all R-homomorphisms from M into N is denoted by M.
The set of all R-homomorphisms from M into N is denoted by
HomR(M,N) or Hom(RM,RN).
For an R-homomorphism f HomR(M,N)
we define its kernel as HomR(M,N)
we define its kernel as
ker(f) = { m
 M | f(m) = 0
}. M | f(m) = 0
}.
We say that f is an isomorphism if it is both one-to-one and onto.
Elements of HomR(M,M) are called endomorphisms, and
isomorphisms in HomR(M,M) are called automorphisms. The set of
endomorphisms of RM will be denoted by
EndR(M).
10.1.4 Proposition. Let M be a free left R-module, with basis X. For any
left R-module N and any function
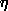 :X->N there
exists a unique R-homomorphism f:M->N with f(x)= :X->N there
exists a unique R-homomorphism f:M->N with f(x)=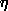 (x),
for all x (x),
for all x X. X.
10.1.5 Theorem. Let N, N0, M0 be submodules of
RM.
(a) N0 / (N0
 M0) M0)
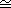 (N0
+ M0) / M0. (N0
+ M0) / M0.
(b) If N0
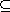 N, then
(M / N0) / (N / N0) N, then
(M / N0) / (N / N0)
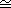 M / N. M / N.
(c) If N0
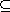 N, then
N N, then
N  (N0
+ M0) = N0 + (N (N0
+ M0) = N0 + (N
 M0). M0).
10.1.6 Lemma. Let X be any subset of the module RM. Any
submodule N with N X X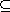 (0)
is contained in a submodule maximal with respect to this property. (0)
is contained in a submodule maximal with respect to this property.
A submodule N of the left R-module M is called a maximal submodule if
N M and for
any submodule K with N M and for
any submodule K with N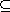 K K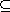 M,
either N=K or K=M. Consistent with this terminology, a left ideal A of R is
called a maximal left ideal if A M,
either N=K or K=M. Consistent with this terminology, a left ideal A of R is
called a maximal left ideal if A R
and for any left ideal B with A R
and for any left ideal B with A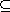 B B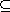 R,
either A=B or B=R. Thus A is maximal precisely when it is a maximal element in
the set of proper left ideals of R, ordered by inclusion. It is an immediate
consequence of Lemma 10.1.6 that every left ideal of the ring R is contained in
a maximal left ideal, by applying the proposition to the set X = {1}.
Furthermore, any left ideal maximal with respect to not including 1 is in fact a
maximal left ideal. R,
either A=B or B=R. Thus A is maximal precisely when it is a maximal element in
the set of proper left ideals of R, ordered by inclusion. It is an immediate
consequence of Lemma 10.1.6 that every left ideal of the ring R is contained in
a maximal left ideal, by applying the proposition to the set X = {1}.
Furthermore, any left ideal maximal with respect to not including 1 is in fact a
maximal left ideal.
10.1.7 Proposition. For any nonzero element m of the module RM
and any submodule N of M with m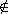 N,
there exists a submodule N* maximal with respect to N* N,
there exists a submodule N* maximal with respect to N*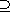 N
and m N
and m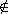 N*.
Moreover, M/N* has a minimal submodule contained in every nonzero submodule. N*.
Moreover, M/N* has a minimal submodule contained in every nonzero submodule.
10.1.8 Corollary. Any proper submodule of a finitely generated module
is contained in a maximal submodule.
10.1.9 Definition. Let R be a ring, and let M be a left R-module. For
any element m M,
the left ideal M,
the left ideal
Ann(m) = { r
 R | r m = 0 } R | r m = 0 }
is called the annihilator of m. The ideal
Ann (M) = { r
 R | r m = 0
for all m R | r m = 0
for all m  M
}. M
}.
is called the annihilator of M.
The module M is called faithful if Ann(M)=(0).
10.1.10 Definition. A nonzero module RM is called simple
(or irreducible) if its only submodules are (0) and M.
We first note that a submodule N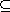 M
is maximal if and only if M/N is a simple module. A submodule N M
is maximal if and only if M/N is a simple module. A submodule N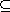 M
is called a minimal submodule if N M
is called a minimal submodule if N (0)
and for any submodule K with N (0)
and for any submodule K with N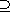 K K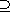 (0),
either N=K or K=(0). With this terminology, a submodule N is minimal if and only
if it is simple when considered as a module in its own right. (0),
either N=K or K=(0). With this terminology, a submodule N is minimal if and only
if it is simple when considered as a module in its own right.
10.1.11 Lemma. [Schur] If RM is simple, then EndR(M)
is a division ring.
10.1.12 Proposition. The following conditions hold for a left R-module
M.
(a) The module M is simple if and only if Rm=M, for each nonzero m M. M.
(b) If M is simple, then Ann(m) is a maximal left ideal, for each nonzero
m M. M.
(c) If M is simple, then it has the structure of a left vector space over
a division ring.
Direct sums and products
10.2.1 Definition. Let {M } }  I be a collection of left R-modules indexed by the set I. The direct
product of the modules {M
I be a collection of left R-modules indexed by the set I. The direct
product of the modules {M } }  I is the Cartesian product
I is the Cartesian product
   IM
IM ,
with componentwise addition and scalar multiplication. That is, if x,y ,
with componentwise addition and scalar multiplication. That is, if x,y    IM
IM ,
with components x ,
with components x ,
y ,
y  M M for all
for all   I, then x+y is defined to be the element with components (x+y)
I, then x+y is defined to be the element with components (x+y) =x =x +y +y ,
for all ,
for all   I. If r
I. If r R, then
rx is defined to be the element with components (rx) R, then
rx is defined to be the element with components (rx) =rx =rx ,
for all ,
for all   I.
I.
The submodule of
   IM
IM consisting of all elements m such that m
consisting of all elements m such that m =0
for all but finitely many components m =0
for all but finitely many components m is called the direct sum of the modules {M
is called the direct sum of the modules {M } }  I, and is denoted by
I, and is denoted by
   IM
IM . .
10.2.2 Proposition. Let {M } }  I be a collection of left R-modules indexed by the set I, and let N be a
left R-module.
I be a collection of left R-modules indexed by the set I, and let N be a
left R-module.
For each   I let p
I let p : :   IM
IM ->M ->M be the projection defined by p
be the projection defined by p (m)=m (m)=m ,
for all m ,
for all m    IM
IM ,
and let i ,
and let i :M :M -> ->   IM
IM be the inclusion defined for all x
be the inclusion defined for all x M M by i
by i (x)=m,
where m (x)=m,
where m =x
and mi=0 for all i =x
and mi=0 for all i  . .
(a) For any set {f } }  I of R-homomorphisms such that f
I of R-homomorphisms such that f :N->M :N->M for each
for each   I, there exists a unique R-homomorphism f:N->
I, there exists a unique R-homomorphism f:N->   IM
IM such that p
such that p f=f f=f for all
for all   I.
I.
(b) For any set {f } }  I of R-homomorphisms such that f
I of R-homomorphisms such that f :M :M ->N
for each ->N
for each   I, there exists a unique R-homomorphism f:
I, there exists a unique R-homomorphism f:   IM
IM ->N
such that fi ->N
such that fi =f =f for each
for each   I.
I.
10.2.3 Proposition. Let M be a left R-module.
(a) The module M is free if and only if it is isomorphic to a direct sum
RI, for some index set I.
(b) The module M is a homomorphic image of a free module.
10.2.4 Proposition. Let M and M1, . . . , Mn be
left R-modules. Then
M 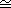 M1 M1
 M2 M2
 . . . . . .
 Mn Mn
if and only if there exist R-homomorphisms ij:Mj->M and pj:M->Mj
for j=1, . . . , n such that
pj ik =
 jk
and i1p1 + . . . + inpn = 1M. jk
and i1p1 + . . . + inpn = 1M.
10.2.5 Proposition. Let A1, A2, . . . , An
be left ideals of the ring R.
(a) R = A1
 A2 A2
 . . . . . .
 An
if and only if there exists a set e1, e2, . . . , en
of orthogonal idempotent elements of R such that Aj=Rej
for 1 An
if and only if there exists a set e1, e2, . . . , en
of orthogonal idempotent elements of R such that Aj=Rej
for 1 j j n
and e1 + e2 + . . . + en = 1. n
and e1 + e2 + . . . + en = 1.
(b) The left ideals Aj in part (a) are two-sided ideals if and
only if the corresponding idempotent elements belong to the center of R.
(c) If condition (b) holds, then every left R-module M can be written as
a direct sum
M=M1
 M2 M2
 . . . . . .
 Mn,
where Mj is a module over the ring Aj, for 1 Mn,
where Mj is a module over the ring Aj, for 1 j j n. n.
10.2.6 Definition. Let L, M, N be left R-modules.
An onto R-homomorphism f:M->N is said to be split if there exists an
R-homomorphism g:N->M with fg=1N.
A one-to-one R-homomorphism g:L->M is said to be split if there exists an
R-homomorphism f:M->L such that fg=1L.
10.2.7 Proposition. Let M, N be left R-modules.
(a) Let f:M->N and g:N->M be R-homomorphisms such that fg=1N.
Then M=ker(f) Im(g). Im(g).
(b) A one-to-one R-homomorphism g:N->M splits if and only if Im(g) is a
direct summand of M.
(c) An onto R-homomorphism f:M->N splits if and only if ker(f) is a
direct summand of M.
10.2.8 Proposition. Let L, M, and N be left R-modules. Let g:L->M be a
one-to-one R-homomorphism, and let f:M->N be an onto R-homomorphism such that
Im(g)=ker(f). Then g is split if and only if f is split, and in this case M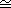 L L N. N.
10.2.9 Corollary. The following conditions are equivalent for the
module RM:
(1) every submodule of M is a direct summand;
(2) every one-to-one R-homomorphism into M splits;
(3) every onto R-homomorphism out of M splits.
10.2.10 Definition. A module RM is called completely
reducible if every submodule of M is a direct summand of M.
10.2.11 Proposition. The following conditions are equivalent for the
module RP:
(1) every R-homomorphism onto P splits;
(2) P is isomorphic to a direct summand of a free module;
(3) for any onto R-homomorphism p:M->N and any R-homomorphism f:P->N
there exists a lifting f*:P->M such that pf*=f.
10.2.12 Definition. A module RM is called projective
if it is isomorphic to a direct summand of a free module.
Chain conditiions
10.3.1 Definition. A module R M is said to be Noetherian
if every ascending chain
M1
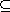 M2 M2
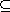 M3 M3
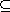 . . . . . .
of submodules of M must terminate after a finite number of steps.
Similarly, M is said to be Artinian if every descending chain
M1
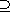 M2 M2
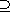 M3 M3
 . . . . . .
of submodules of M must terminate after a finite number of steps.
10.3.2 Definition. A ring R is said to be left Noetherian if
the module RR is Noetherian.
A ring R is said to be left Artinian if the module RR is
Artinian.
If R satisfies the conditions for both right and left ideals, then it is simply
said to be Noetherian or Artinian.
10.3.3 Proposition. The following conditions are equivalent for a
module RM:
(1) M is Noetherian;
(2) every submodule of M is finitely generated;
(3) every nonempty set of submodules of M has a maximal member.
10.3.4 Proposition. The following conditions hold for a module RM
and any submodule N.
(a) M is Noetherian if and only if N and M/N are Noetherian.
(b) M is Artinian if and only if N and M/N are Artinian.
10.3.5 Corollary. A finite direct sum of modules is Noetherian if and
only if each summand is Noetherian; it is Artinian if and only if each summand
is Artinian.
10.3.6 Proposition. A ring R is left Noetherian if and only if every
finitely generated left R-module is Noetherian; it is left Artinian if and only
if every finitely generated left R-module is Artinian.
10.3.7 Theorem. [Hilbert basis theorem] If R is a left Noetherian
ring, then so is the polynomial ring R[x].
10.3.8 Definition. Let D be a principal ideal domain. and left M be a
D-module. We say that M is a torsion module if Ann(m) (0)
for all nonzero elements m (0)
for all nonzero elements m M. M.
10.3.9 Proposition. Let D be a principal ideal domain. Any finitely
generated torsion D-module has finite length.
We can now give some fairly wide classes of examples of Noetherian and
Artinian rings. If D is a principal ideal domain, then D is Noetherian since
each ideal is generated by a single element. It follows that the polynomial ring
D[x1,x2,...,xn] is also Noetherian. If F is a
field, then F[x]/I is Artinian, for any nonzero ideal I of F[x], since F[x] is a
principal ideal domain. This allows the construction of many interesting
examples. Note that D[x]/I need not be Artinian when D is assumed to be a
principal ideal domain rather than a field, since Z[x]/<x> is
isomorphic to Z, which is not Artinian.
|

