Principal ideal domains
9.1.1. Definition. An integral domain D is called a Euclidean domain
if for each nonzero element x in D there is assigned a nonnegative integer
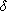 (x) such
that (x) such
that
- (i)
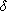 (ab) (ab)

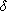 (b)
for all nonzero a,b in D, and (b)
for all nonzero a,b in D, and
- (ii) for any nonzero elements a,b in D there exist q,r in D such
that a = bq + r,
where either r = 0 or
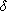 (r) < (r) <
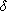 (b). (b).
9.1.2. Theorem. Any Euclidean domain is a principal ideal domain.
Let a and b be elements of a commutative ring R with 1. Then a is called an
associate of b if a = bu for some unit u in R.
9.1.4. Definition. Let a and b be elements of a commutative ring R
with identity. An element d of R is called a greatest common divisor of a
and b if
- (i) d | a and d | b, and
- (ii) if c | a and c | b, for c in R, then c | d.
9.1.6. Proposition. Let D be a principal ideal domain. If a and b are
nonzero elements of D, then D contains a greatest common divisor of a and b, of
the form as+bt for s,t in D. Furthermore, any two greatest common divisors of a
and b are associates.
In the situation of the above proposition, in an integral domain D, we say
that a and b are relatively prime if aD+bD=D.
9.1.7. Definition. Let R be a commutative ring with identity. A
nonzero element p of R is said to be irreducible if
- (i) p is not a unit of R, and
- (ii) if p = ab for a,b in R, then either a or b is a unit of R.
9.1.8. Proposition. Let p be an irreducible element of the principal
ideal domain D. If a,b
 D and p|ab,
then either p|a or p|b. D and p|ab,
then either p|a or p|b.
9.1.9. Proposition. Let D be a principal ideal domain, and let p be a
nonzero element of D. Then p is irreducible in D if and only if pD is a prime
ideal of D.
9.1.10. Definition. Let D be an integral domain. Then D is called a
unique factorization domain if
- (i) each nonzero element a of D that is not a unit can be
expressed as a product of irreducible elements of D, and
- (ii) in any two such factorizations a = p1 p2
� � � pn = q1 q2 � � � qm the
integers n and m are equal and it is possible to rearrange the factors so
that qi is an associate of pi, for 1
 i i
 n. n.
9.1.11. Lemma. Let D be a principal ideal domain. In any collection of
ideals
I 1
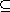 I
2 I
2 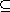 I 3
I 3
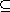 � � � , � � � ,
there is a subscript m such that In = Im for all n>m.
9.1.12. Theorem. Any principal ideal domain is a unique factorization
domain.
Unique factorization domains
9.2.1. Lemma. Let D be a unique factorization domain, and let p be an
irreducible element of D. If a,b
 D and p|ab,
then p|a or p|b. D and p|ab,
then p|a or p|b.
9.2.2. Definition. Let D be a unique factorization domain. A
nonconstant polynomial
f(x) = an xn + an-1 xn-1 + � � � + a1
x + a0 in D[x] is called primitive if there is no irreducible
element p in D such that p | ai for all i.
9.2.3. Lemma. The product of two primitive polynomials is primitive.
9.2.4. Lemma. Let Q be the quotient field of D, and let f(x)
 Q[x]. Then
f(x) can be written in the form f(x) = (a/b)f*(x), where f*(x) is a primitive
element of D[x], a,b Q[x]. Then
f(x) can be written in the form f(x) = (a/b)f*(x), where f*(x) is a primitive
element of D[x], a,b
 D, and a and
b have no common irreducible divisors. This expression is unique, up to units of
D. D, and a and
b have no common irreducible divisors. This expression is unique, up to units of
D.
9.2.5. Lemma. Let D be a unique factorization domain, let Q be the
quotient field of D, and let f(x) be a primitive polynomial in D[x]. Then f(x)
is irreducible in D[x] if and only if f(x) is irreducible in Q[x].
9.2.6. Theorem. If D is a unique factorization domain, then so is the
ring D[x] of polynomials with coefficients in D.
9.2.7. Corollary. For any field F, the ring of polynomials
F[x1 , x2 , ... , xn]
in n indeterminates is a unique factorization domain.
Example. 9.2.1. The ring Z [
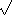 -5 ] is not
a unique factorization domain. -5 ] is not
a unique factorization domain.
|

