Minimum and Maximum Values

Minimum and Maximum Values

Many of our applications in this chapter will revolve around minimum and maximum values of a function. While we can all visualize the minimum and maximum values of a function we want to be a little more specific in our work here. In particular we want to differentiate between two types of minimum or maximum values. The following definition gives the types of minimums and/or maximums values that we�ll be looking at.

Definition

Note that when we say an �open interval around � we mean that we can find some interval , not including the endpoints, such that . Or, in other words, c will be contained somewhere inside the interval and will not be either of the endpoints.

Also, we will collectively call the minimum and maximum points of a function the extrema of the function. So, relative extrema will refer to the relative minimums and maximums while absolute extrema refer to the absolute minimums and maximums.

Now, let�s talk a little bit about the subtle difference between the absolute and relative in the definition above.

We will have an absolute maximum (or minimum) at provided f(c) is the largest (or smallest) value that the function will ever take on the domain that we are working on. Also, when we say the �domain we are working on� this simply means the range of x�s that we have chosen to work with for a given problem. There may be other values of x that we can actually plug into the function but have excluded them for some reason.

A relative maximum or minimum is slightly different. All that�s required for a point to be a relative maximum or minimum is for that point to be a maximum or minimum in some interval of x�s around . There may be larger or smaller values of the function at some other place, but relative to , or local to , f(c) is larger or smaller than all the other function values that are near it.

Note as well that in order for a point to be a relative extrema we must be able to look at function values on both sides of to see if it really is a maximum or minimum at that point. This means that relative extrema do not occur at the end points of a domain. They can only occur interior to the domain.

There is actually some debate on the preceding point. Some folks do feel that relative extrema can occur on the end points of a domain. However, in this class we will be using the definition that says that they can�t occur at the end points of a domain.

It�s usually easier to get a feel for the definitions by taking a quick look at a graph.

For the function shown in this graph we have relative maximums at and . Both of these point are relative maximums since they are interior to the domain shown and are the largest point on the graph in some interval around the point. We also have a relative minimum at since this point is interior to the domain and is the lowest point on the graph in an interval around it. The far right end point, , will not be a relative minimum since it is an end point.

The function will have an absolute maximum at and an absolute minimum at . These two points are the largest and smallest that the function will ever be. We can also notice that the absolute extrema for a function will occur at either the endpoints of the domain or at relative extrema. We will use this idea in later sections so it�s more important than it might seem at the present time.

Let�s take a quick look at some examples to make sure that we have the definitions of absolute extrema and relative extrema straight.

Example Identify the absolute extrema and relative extrema for the following function.

Solution

Since this function is easy enough to graph let�s do that. However, we only want the graph on the interval [-1,2]. Here is the graph,

Note that we used dots at the end of the graph to remind us that the graph ends at these points.

We can now identify the extrema from the graph. It looks like we�ve got a relative and absolute minimum of zero at 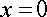and an absolute maximum of four at . Note that is not a relative maximum since it is at the end point of the interval.

This function doesn�t have any relative maximums.