Algebraic form.
A complex number is an expression of the form
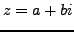 , where
, where
 are real numbers and
are real numbers and
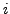 is a ``number'' such that
is a ``number'' such that
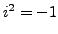 . The number
. The number
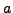 is called the real part of
is called the real part of
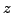
(
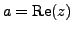 ) and
) and
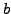 is the imaginary part (or imaginary coefficient) of
is the imaginary part (or imaginary coefficient) of
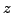 (
(
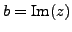 ).
).
The set of all complex numbers is denoted
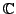 . We denote
. We denote
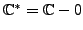 .
.
Properties:
- Equality:
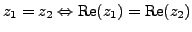 and
and
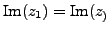 .
.
-
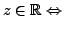 Im
Im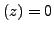 .
.
- If
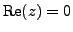 ,
,
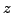 is called pure imaginary.
is called pure imaginary.
Example 1.1.1
-
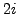 is pure imaginary.
is pure imaginary.
-
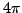 is real.
is real.
Definition 1.1.2
(Operations) Let
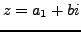
and
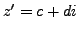
.
- Addition:
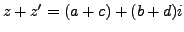 .
.
- Multiplication:
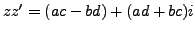 .
.
Example 1.1.3
(Maple writing) : Z1 := 2 + 5*I:
Z2 := 3 - 7*I:
z[1] = Z1;
z[2] = Z2; ` `;
z[1]+z[2]=Z1+Z2;
z[1]*z[2] = Z1*Z2;
These operations have the same algebraic properties as the corresponding
operations in
 (associativity, commutativity, etc.; please prove ...). Thus, the classical
formulas (such as Newton's binomial) are also true in
(associativity, commutativity, etc.; please prove ...). Thus, the classical
formulas (such as Newton's binomial) are also true in
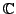 .
.
It is possible to use Maple to verify these laws (associativity,
commutativity, etc.). Here a a few examples:
- : Associativity: Z1 := x[1] + I*y[1]: `z1 ` = Z1;
Z2 := x[2] + I*y[2]: `z2 ` = Z2;
Z3 := x[3] + I*y[3]: `z3 ` = Z3;
w1 := Z1*(Z2 + Z3):
w2 := Z1*Z2 + Z1*Z3: ` `;
`z1*(z2 + z3) ` = w1;
`z1*z2 + z1*z3 ` = w2;
w1 := expand(w1):
w2 := expand(w2): ` `;
`z1*(z2 + z3) ` = w1;
`z1*z2 + z1*z3 ` = w2; ` `;
`Does z1*(z2 + z3) = z1*z2 + z1*z3 �;
evalb(w1 = w2);
- Commutativity: Z1:='Z1': Z1 := x[1] + I*y[1]:
Z2:='Z2': Z2 := x[2] + I*y[2]:
z[1] = Z1;
z[2] = Z2; ` `;
`z1 + z2` = Z1 + Z2;
`z2 + z1` = Z2 + Z1; ` `;
`Does z1 + z2 = z2 + z1 �;
Z1+Z2 = Z2+Z1;
evalb(Z1+Z2 = Z2+Z1);
Example 1.1.7
(With Maple) Z1 := 3 + 2*I:
z[1] = Z1;
conjugate(z[1]) = conjugate(Z1); ` `;
Z2 := -7 + 5*I:
z[2] = Z2;
conjugate(z2) = conjugate(Z2);
Proposition 1.1.8
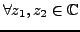 :
:
(i)
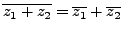 .
.
(ii)
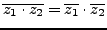 .
.
Proof. Denote
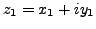
and
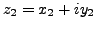
, where
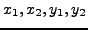
are real numbers. Then:
(i)
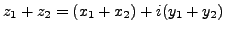 , thus:
, thus:
(ii)
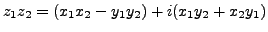 , thus:
, thus:
The following proposition is very simple; we leave the task of proving it to
the reader.
Proposition 1.1.9
Let
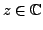 . Then:
. Then:
-
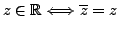 .
.
-
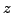 is pure imaginary if, and only if,
is pure imaginary if, and only if,
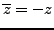 .
.
Definition 1.1.11
(Inverse of a complex) If
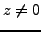
, then it has a complex inverse
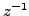
. Let
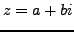
, where
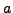
and
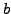
are real numbers; then we have:
Proof.
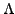
In other words, we have:
Proof.
(i)
If
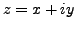 , with real
, with real
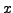 and
and
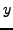 , we have:
, we have:
(ii)
If
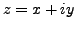 , with real
, with real
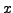 and
and
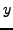 , we have:
, we have:
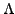
The property in Proposition 1.13
(ii) justifies the following definition:
Definition 1.1.14
(Absolute value)
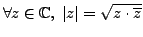
.
For
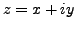 , where
, where
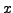 and
and
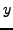 are real numbers, we have:
are real numbers, we have:
Proof. We denote
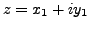
and
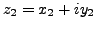
, where
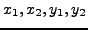
are real numbers.
(i)
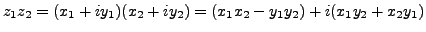 , thus on the one hand, we have:
, thus on the one hand, we have:
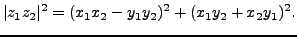 |
(1.1) |
On the other hand, we have:
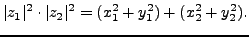 |
(1.2) |
We develop the right-hand sides of Equation
1 and
of Equation
2 and
the required equality follows.
(ii)
We can leave it to the reader. Section
2 explains why it is possible here to use results from analytic
geometry.
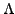
Example 1.1.17
If
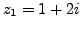
and
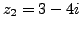
,
Then we have:
The proof is an easy consequence of Proposition 1.16.
Here the proof is an easy consequence of Corollary 1.18
and Proposition 1.16.
Remark 1.1.20
For any
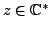
, we have:
It follows that the best way to compute a quotient is to multiply both the
numerator and the denominator by the conjugate of the denominator, and then
simplify.

