Analytic functions
The simplest open neighborhood of a point
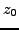is an open ball centered at
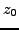; we will generally use such balls.
Definition 3.5.2
Let
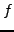
be a function defined over an open subset
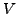
of
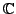
. the function
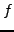
is analytic over
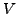
if it is analytic at each point of
.
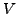
A function which is analytic over the whole of
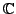is called an entire function.
Proposition 3.5.3
- A polynomial function is analytic at every point of
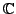, i.e. is an entire function.
- A rational function is analytic at each point of its domain.
Proof.
- A polynomial function is an entire function, as a consequence of
Proposition 2.4
and Ex. 2.3.
- We use once again Proposition 2.4,
together with the previous alinea, as a rational function is the
quotient of two polynomial functions.
Example 3.5.4
Let
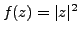
, i.e.
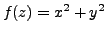
(i.e.
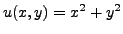
and
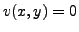
). Then:
C-R equations mean here
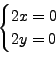, i.e.
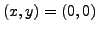. Thus, the origin is the only point where
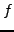can be derivable and
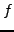is nowhere analytic.
Example 3.5.5
We use the function and the results of Example
3.5. For any point
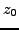
on one of these axes, any open ball centered at
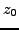
contains points where
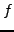
is not differentiable. Thus,
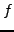
is not analytic at any point.
Example 3.5.6
If
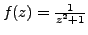
, the function
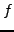
is analytic at every point of
:
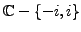
Example 3.5.7
Let
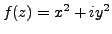
, i.e.
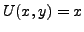
and
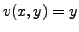
. We have:
Thus, Cauchy-Rieman equations are verified if, and only if,
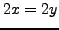
, i.e.
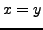
. It follows that
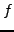
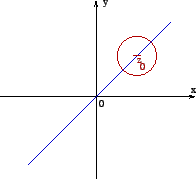
can be derivable only on the line whose equation is
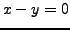
. For any point
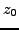
on this line, every non empty open ball centered at
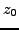
has points out of the line, therefore
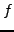
cannot be analytic anywhere (see Figure 3).
Figure 3: Why a function is
nowhere analytic.
 |
|
