Application to integrals | Complex Analysis | Mathematics | GATE Material | GATE Papers | GATE Preparation

Application to integrals

Application to integrals

Application to integrals.

Theorem 9.2.1 (Residue Theorem) Let 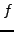be a function, analytic at all the interior points of a Jordan curve 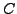, excepted a finite number of isolated singular points 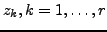$z_k, k=1, \dots , r$ . Then:

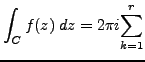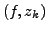$\displaystyle \int_C f(z) \; dz = 2 \pi i \underset{k=1}{{\overset{r}{\sum}}}$ Res $\displaystyle (f, z_k)$

Note that:

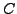is oriented in the positive direction.
Only the interior singularities are involved.

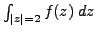
Example 9.2.2 We wish to compute the integral $\int_{\vert z\vert=2} f(z) \; dz$ , where

$\displaystyle f(z)= \frac {e^z}{(z-1)^2(z-i)(z-3)^3}.$

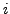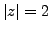The function has a pole of order 1 at , a pole of order 2 at1 and a pole of order 3 at 3; this last pole is irrelevant to our computation as it lies out of the Jordan curve defined by $\vert z\vert=2$ . So we compute two residues:

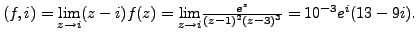
Res $(f,i)= \underset{z \rightarrow i}{\text{lim}} (z-i)f(z) = \underset{z \rightarrow i}{\text{lim}} \frac {e^z}{(z-1)^2(z-3)^3}= 10^{-3}e^i(13-9i).$
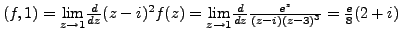
Res $(f,1)= \underset{z \rightarrow 1}{\text{lim}} \frac {d}{dz} (z-i)^2f(z) = \und... ...arrow 1}{\text{lim}} \frac {d}{dz} \frac {e^z}{(z-i)(z-3)^3} = \frac{e}{8}(2+i)$

Thus:

$\displaystyle \int_{\vert z\vert=2} f(z) = 2 \pi i \left( 10^{-3}e^i(13-9i) + \frac{e}{8}(2+i) \right)$

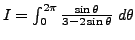
Example 9.2.3 Compute the integral $I= \int_{0}^{2 \pi} \frac {\sin \theta}{3-2 \sin \theta} \; d \theta$ .

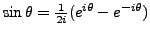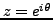We use 2.1: $\sin \theta = \frac {1}{2i} (e^{i \theta} - e^{-i \theta})$ . If $z= e^{i \theta}$ , we have

$\displaystyle I$	$\displaystyle = \int_{\vert z\vert=1} \frac {\frac {1}{2i} (z-z^{-1})}{ 3 - 2 \frac {1}{2i} (z - z^{-1})} \; dz$
$\displaystyle \quad$	$\displaystyle = \int_{\vert z\vert=1} \frac {z-z^{-1}}{6i - 2 (z-z^{-1}} \; dz$
$\displaystyle \quad$	$\displaystyle = \int_{\vert z\vert=1} \frac {z^2-1}{-2z^2 +6i z + 2} \; dz$

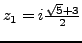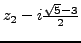The denominator has two complex roots $z_1=i\frac {\sqrt{5}+3}{2}$ and $z_2-i\frac {\sqrt{5}-3}{2}$ . Only the second one is a point interior to the unit-circle, i.e. it is the only pole of the function we have to deal with. Therefore:

$\displaystyle I$	$\displaystyle = 2 \pi i$ Res $\displaystyle [f(z), z_2]$
$\displaystyle \quad$	$\displaystyle = 2 \pi i \underset{z \rightarrow z_2}{\text{lim}} (z-z_2)f(z)$
$\displaystyle \quad$	$\displaystyle = 2 \pi i \underset{z \rightarrow z_2}{\text{lim}} \frac {z^2-1}{-2 \left(z+ \frac {\sqrt{5}-3}{2} i \right) }$
$\displaystyle \quad$	$\displaystyle = \frac {3\sqrt{5}-5}{5} \pi.$